有限加法族の演習問題 22 問(解答付き)|測度論
有限加法族に関する演習問題を解けるようになる。
- 集合 $X$ のべき集合を $\mc{P}(X)$ で表す。
- 全体集合 $X$ が定まっているとき、$A \subseteq X$ の補集合 $X \setminus A$ を単に $\overline{A}$ と書く。
- $\NN$ を非負整数全体の集合とする。
有限加法族(集合代数)の定義
集合 $X$ の部分集合からなる集合 $\mc{F} \subseteq \mc{P}(X)$ が3条件
非空性
$\mc{F} \neq \varnothing$
補集合で閉じる
$A \in \mc{F} \implies \overline{A} \in \mc{F}$
有限和で閉じる
$A, B \in \mc{F} \implies A \cup B \in \mc{F}$
を満たすとき、$\mc{F}$ を $X$ 上の有限加法族と呼ぶ。
$X = \cbr{1,2,3}$ に対し、 $$\mc{F} = \cbr{\varnothing, \cbr{1}, \cbr{2, 3}, \cbr{1,2,3}}$$ は $X$ 上の有限加法族。
有限加法族が満たす基本的な性質
補集合・有限和・有限交叉・差集合
といった集合演算で閉じる
$(A \cup \overline{B}) \cap (C \setminus A)$ も $\mc{F}$ に属す
有限加法族は全体集合を要素に持つことを示せ。つまり $\mc{F}$ が集合 $X$ 上の有限加法族ならば
全体集合を持つ
$X \in \mc{F}$
$\mc{F} \neq \varnothing$ なので $A_0 \in \mc{F}$ を一つ取れる。$\mc{F}$ は補集合で閉じているので $$\overline{A_0} \in \mc{F}$$ である。更に $\mc{F}$ は有限和でも閉じているので $$A_0 \cup \overline{A_0} \in \mc{F}$$ である。すなわち $X \in \mc{F}$ である。
有限加法族は空集合を要素に持つことを示せ。つまり $\mc{F}$ が集合 $X$ 上の有限加法族ならば
空集合を持つ
$\varnothing \in \mc{F}$
有限加法族は全体集合を要素に持つ(問題1)ので $$X \in \mc{F}$$ である。また $\mc{F}$ は補集合で閉じるので $$\overline{X} \in \mc{F}$$ である。すなわち $\varnothing \in \mc{F}$ である。
有限加法族は有限交叉で閉じることを示せ。つまり $\mc{F}$ が集合 $X$ 上の有限加法族ならば
有限交叉で閉じる
$A, B \in \mc{F} \implies A \cap B \in \mc{F}$
$A, B \in \mc{F}$ とする。$A \cap B = \overline{\overline{A} \cup \overline{B}}$ であることに注意。 $\mc{F}$ は補集合で閉じているので $$\overline{A}, \overline{B} \in \mc{F}$$ である。また $\mc{F}$ は有限和で閉じているので $$\overline{A} \cup \overline{B} \in \mc{F}$$ である。更に $\mc{F}$ は補集合で閉じているので $$\overline{\overline{A} \cup \overline{B}} \in \mc{F}$$ である。すなわち $A \cap B \in \mc{F}$ である。
有限加法族は差集合で閉じることを示せ。つまり $\mc{F}$ が集合 $X$ 上の有限加法族ならば
差集合で閉じる
$A, B \in \mc{F} \implies A \setminus B \in \mc{F}$
$A, B \in \mc{F}$ とする。$A \setminus B = A \cap \overline{B}$ であることに注意。$\mc{F}$ は補集合で閉じているので $$\overline{B} \in \mc{F}$$ である。また $\mc{F}$ は有限交叉で閉じているので(問題3) $$A \cap \overline{B} \in \mc{F}$$ である。すなわち $A \setminus B \in \mc{F}$ である。
その有限加法族に属す
無限回の操作に対してどうなるか……
という話は後程
有限加法族の例
集合 $X$ に対し $$\mc{F} = \cbr{\varnothing, X}$$ は $X$ 上の有限加法族であることを示せ。
非空性は自明。
\begin{align} \overline{\varnothing} = X \in \mc{F} && \overline{X} = \varnothing \in \mc{F} \end{align}
\begin{align} \varnothing \cup \varnothing = \varnothing \in \mc{F} && \varnothing \cup X = X \in \mc{F} \end{align} \begin{align} X \cup \varnothing = X \in \mc{F} && X \cup X = X \in \mc{F} \end{align}
集合 $X$ とその部分集合 $S$ に対し、 $$\mc{F} = \cbr{\varnothing, S, \overline{S}, X}$$ は $X$ 上の有限加法族であることを示せ。
非空性は自明。
\begin{align} \overline{\varnothing} = X \in \mc{F} && \phantom{\overline{\varnothing} ={}} \overline{S} \in \mc{F} \end{align} \begin{align} \overline{\overline{S}} = S \in \mc{F} && \overline{X} = \varnothing \in \mc{F} \end{align}
$A, B \in \mc{F}$ として $A \cup B \in \mc{F}$ を示す。
\begin{align} &\text{$A = \varnothing$ のとき:} & & A \cup B = B \in \mc{F} \\ &\text{$B = \varnothing$ のとき:} & & A \cup B = A \in \mc{F} \\ &\text{$A = X$ または $B = X$ のとき:} & & A \cup B = X \in \mc{F} \\ &\text{$A = B$ のとき:} & & A \cup B = A \in \mc{F} \\ &\text{$A = S$ かつ $B = \overline{S}$ のとき:} & & A \cup B = X \in \mc{F} \\ &\text{$A = \overline{S}$ かつ $B = S$ のとき:} & & A \cup B = X \in \mc{F} \end{align}集合 $X$ に対し、 $$\mc{F} = \mc{P}(X)$$ は $X$ 上の有限加法族であることを示せ。
$X$ の部分集合はみな $\mc{F}$ の要素なので補集合・有限和で閉じることは自明。
また $\varnothing \in \mc{F}$ なので $\mc{F} \neq \varnothing$ である。
$\mc{P}(\varnothing) = \varnothing$ じゃなくて $\mc{P}(\varnothing) = \cbr{\varnothing}$
$\mc{P}(\varnothing)$ は $\varnothing$ を要素に持つでしょ
集合 $X = \cbr{1,2,3}$ の部分集合からなる集合 $$\mc{F} = \cbr{\varnothing, \cbr{1}, \cbr{1, 2}, \cbr{1,2,3}}$$ は $X$ 上の有限加法族か?
$X$ 上の有限加法族ではない。実際、$\cbr{1} \in \mc {F}$ であるが、 $$\overline{\cbr{1}} = \cbr{2,3} \not\in\mc{F}$$ であるので $\mc{F}$ は補集合で閉じていない。したがって有限加法族ではない。
$X$ 上の有限加法族ではない。実際、$\cbr{1}, \cbr{1, 2} \in \mc {F}$ であるが、 $$\cbr{1,2} \setminus \cbr{1} = \cbr{2} \not\in\mc{F}$$ なので $\mc{F}$ は差集合で閉じていない。したがって有限加法族ではない(問題4)。
$\NN$ の部分集合からなる集合 $$\mc{F} = \iset{S \subseteq \NN}{\text{$S$ または $\overline{S}$ は有限集合}}$$ は $\NN$ 上の有限加法族であることを示せ。
$\varnothing \in \mc{F}$ なので $\mc{F} \neq \varnothing$ である。
$A \in \mc{F}$ とする。$\mc{F}$ の定義より $A$ か $\overline{A}$ のどちらかが有限集合。
$\overline{\overline{A}}$ が有限集合なので $\overline{A} \in \mc{F}$ である。
$\mc{F}$ の定義より $\overline{A} \in \mc{F}$ である。
$A, B \in \mc{F}$ とする。$A$ と $\overline{A}$ のどちらかが有限集合で、$B$ と $\overline{B}$ のどちらかが有限集合。
$A \cup B$ が有限集合となるので $A \cup B \in \mc{F}$ である。
$\overline{A} \cap \overline{B}$ が有限集合、すなわち $\overline{A \cup B}$ が有限集合なので $A \cup B \in \mc{F}$ である。
$\RR$ の部分集合からなる集合 $$\mc{F} = \iset{S \subseteq \RR}{\text{$S$ または $\overline{S}$ は高々可算集合}}$$ は $\RR$ 上の有限加法族であることを示せ。
$\NN \in \mc{F}$ なので $\mc{F} \neq \varnothing$ である。
$A \in \mc{F}$ として $\overline{A} \in \mc{F}$ を示す。$\mc{F}$ の定義より $A$ または $\overline{A}$ が高々可算集合。
$\overline{\overline{A}}$ が高々可算集合となるので $\overline{A} \in \mc{F}$ である。
$\mc{F}$ の定義より $\overline{A} \in \mc{F}$ である。
$A, B \in \mc{F}$ として $A \cup B \in \mc{F}$ を示す。$A$ と $\overline{A}$ のどちらかが高々可算集合で、$B$ と $\overline{B}$ のどちらかが高々可算集合。
$A \cup B$ が高々可算集合となるので $A \cup B \in \mc{F}$ である。
$\overline{A} \cap \overline{B}$ が高々可算集合、すなわち $\overline{A \cup B}$ が高々可算集合なので $A \cup B \in \mc{F}$ である。
$\NN$ の部分集合で加法で閉じるもの全体、すなわち $$\mc{F} = \iset{S \subseteq \NN}{\text{任意の $x, y \in S$ に対し $x + y \in S$}}$$ は $\NN$ 上の有限加法族か?
有限加法族ではない。実際、$S_2 = \iset{2m}{m \in \NN}$ については $$2m_1 + 2m_2 = 2(m_1 + m_2) \in S_2$$ なので $S_2 \in \mc{F}$ であるが、一方 $\overline{S_2}$ については \begin{align} 1, 3 &\in \overline{S_2} & 1 + 3 = 4 &\not\in \overline{S_2} \end{align} なので $\overline{S_2} \not\in \mc{F}$ である。つまり $\mc{F}$ は補集合で閉じていない。
有限加法族ではない。実際、$S_2 = \iset{2m}{m \in \NN}$ については $$2m_1 + 2m_2 = 2(m_1 + m_2) \in S_2$$ なので $S_2 \in \mc{F}$ であり、また同様にして $S_3 = \iset{3m}{m \in \NN} \in \mc{F}$ であるが、$S_2 \cup S_3$ については \begin{align} 2, 3 &\in S_2 \cup S_3 & 2 + 3 = 5 &\not\in S_2 \cup S_3 \end{align} なので $S_2 \cup S_3 \not\in \mc{F}$ である。つまり $\mc{F}$ は有限和で閉じていない。
$\NN$ の部分集合で乗法で閉じるもの全体、すなわち $$\mc{F} = \iset{S \subseteq \NN}{\text{任意の $x, y \in S$ に対し $xy \in S$}}$$ は $\NN$ 上の有限加法族か?
有限加法族ではない。実際、$S_2 = \iset{m^2}{m \in \NN}$ については $$m_1^2 \cdot m_2^2 = (m_1 m_2)^2 \in S_2$$ なので $S_2 \in \mc{F}$ であるが、一方 $\overline{S_2}$ については \begin{align} 2 &\in \overline{S_2} & 2 \cdot 2 = 4 &\not\in \overline{S_2} \end{align} なので $\overline{S_2}$ は $\mc{F}$ に属さない。つまり $\mc{F}$ は補集合で閉じていない。
有限加法族ではない。実際、$S_2 = \iset{m^2}{m \in \NN}$ については $$m_1^2 \cdot m_2^2 = (m_1 m_2)^2 \in S_2$$ なので $S_2 \in \mc{F}$ であり、また同様に $S_3 = \iset{m^3}{m \in \NN} \in \mc{F}$ であるが、$S_2 \cup S_3$ については \begin{align} 4, 8 &\in S_2 \cup S_3 & 4 \cdot 8 = 32 &\not\in S_2 \cup S_3 \end{align} なので $S_2 \cup S_3$ は $\mc{F}$ に属さない。つまり $\mc{F}$ は補集合で閉じていない。
有限加法族になるための条件
「非空性」「補集合で閉じる」「有限和で閉じる」
の三つを確かめる方法の他に
どんな方法があるのか
……ということについて考えてみよう
集合 $X$ の部分集合からなる集合 $\mc{F} \subseteq \mc{P}(X)$ が3条件
非空性
$\mc{F} \neq \varnothing$
補集合で閉じる
$A \in \mc{F} \implies \overline{A} \in \mc{F}$
有限交叉で閉じる
$A, B \in \mc{F} \implies A \cap B \in \mc{F}$
を満たせば $\mc{F}$ は有限加法族であることを示せ。
有限和で閉じることを示す。$A, B \in \mc{F}$ とする。$A \cup B = \overline{\overline{A} \cap \overline{B}}$ であることに注意。
$\mc{F}$ は補集合で閉じているので $$\overline{A}, \overline{B} \in \mc{F}$$ である。また $\mc{F}$ は有限交叉で閉じているので $$\overline{A} \cap \overline{B} \in \mc{F}$$ である。更に $\mc{F}$ は補集合で閉じているので $$\overline{\overline{A} \cap \overline{B}} \in \mc{F}$$ である。すなわち $A \cup B \in \mc{F}$ である。
集合 $X$ の部分集合からなる集合 $\mc{F} \subseteq \mc{P}(X)$ が2条件
全体集合を持つ
$X \in \mc{F}$
差集合で閉じる
$A, B \in \mc{F} \implies A \setminus B \in \mc{F}$
を満たせば $\mc{F}$ は有限加法族であることを示せ。
$X \in \mc{F}$ より $\mc{F} \neq \varnothing$ である。
$A \in \mc{F}$ とする。いま $X \in \mc{F}$ であり、また $\mc{F}$ は差集合で閉じているので $$X \setminus A \in \mc{F}$$ である。すなわち $\overline{A} \in \mc{F}$ である。
$A, B \in \mc{F}$ とする。$A \cup B = \overline{\overline{B} \setminus A}$ であることに注意。
いま示したように $\mc{F}$ は補集合で閉じているので $$\overline{B} \in \mc{F}$$ である。また $\mc{F}$ は差集合で閉じているので $$\overline{B} \setminus A \in \mc{F}$$ である。更に $\mc{F}$ は補集合で閉じているので $$\overline{\overline{B} \setminus A} \in \mc{F}$$ である。すなわち $A \cup B \in \mc{F}$ である。
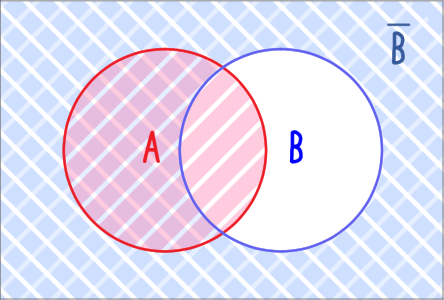
集合 $X$ の部分集合からなる集合 $\mc{F} \subseteq \mc{P}(X)$ が2条件
非空性
$\mc{F} \neq \varnothing$
差集合で閉じる
$A, B \in \mc{F} \implies A \setminus B \in \mc{F}$
を満たせば $\mc{F}$ は有限加法族であると言えるか?
そうとは限らない。実際 $X = \cbr{1}$ および $\mc{F} = \cbr{\varnothing}$ とすると、$\mc{F}$ は非空であり、また $\varnothing \setminus \varnothing = \varnothing \in \mc{F}$ なので差集合で閉じてもいるが、$\mc{F}$ は全体集合 $\cbr{1}$ を要素として持たないので有限加法族ではない。
集合 $X$ の部分集合からなる集合 $\mc{F} \subseteq \mc{P}(X)$ が2条件
非空性
$\mc{F} \neq \varnothing$
交叉の否定で閉じる
$A, B \in \mc{F} \implies \overline{A \cap B} \in \mc{F}$
を満たせば $\mc{F}$ は有限加法族であることを示せ。
非空性は自明。補集合・有限和で閉じていることを示す。
$A \in \mc{F}$ とする。$\mc{F}$ は交叉の否定で閉じているので $$\overline{A \cap A} \in \mc{F}$$ である。すなわち $\overline{A} \in \mc{F}$ である。
$A, B \in \mc{F}$ とする。$A \cup B = \overline{\overline{A} \cap \overline{B}}$ であることに注意。
いま示した通り $\mc{F}$ は補集合で閉じているので $$\overline{A}, \overline{B} \in \mc{F}$$ である。また $\mc{F}$ は交叉の否定で閉じているので $$\overline{\overline{A} \cap \overline{B}} \in \mc{F}$$ である。すなわち $A \cup B \in \mc{F}$ である。
何か通じるものを感じる……
有限加法族から有限加法族を作る
集合 $X$ の部分集合からなる集合 $\mc{F}_1, \mc{F}_2$ に対し、
$\mc{F}_1$ も $\mc{F}_2$ も有限加法族ならば $\mc{F}_1 \cup \mc{F}_2$ も有限加法族
は一般に成り立つか?一般には成り立たない。実際 $X = \cbr{1, 2, 3}$ とし、 $$\mc{F}_1 = \cbr{\varnothing, \cbr{1}, \cbr{2, 3}, X}$$ $$\mc{F}_2 = \cbr{\varnothing, \cbr{1, 2}, \cbr{3}, X}$$ とすると、これらは有限加法族である(問題6)。しかし $$\mc{F}_1 \cup \mc{F}_2 = \cbr{\varnothing, \cbr{1}, \cbr{1, 2}, \cbr{2, 3}, \cbr{3}, X}$$ において、$\cbr{1}, \cbr{3} \in \mc{F}_1 \cup \mc{F}_2$ であるが $$\cbr{1} \cup \cbr{3}= \cbr{1,3} \not\in \mc{F}_1 \cup \mc{F}_2$$ なので $\mc{F}_1 \cup \mc{F}_2$ は有限和で閉じていない。したがって $\mc{F}_1 \cup \mc{F}_2$ は有限加法族ではない。
集合 $X$ の部分集合からなる集合の族 $\cbr{\mc{F}_\lambda}_{\lambda \in \Lambda}$ (ただし $\Lambda \neq \varnothing$(※) )に対し、
どの $\lambda \in \Lambda$ についても $\mc{F}_\lambda$ が有限加法族ならば $\ds\bigcap_{\lambda \in \Lambda} \mc{F}_\lambda$ も有限加法族
であることを示せ。$\ds\mc{F} = \bigcap_{\lambda \in \Lambda} \mc{F}_\lambda$ とする。
任意の $\lambda \in \Lambda$ に対し $\varnothing \in \mc{F}_\lambda$ なので $\varnothing \in \mc{F}$ である。特に $\mc{F} \neq \varnothing$ である。
$A \in \mc{F}$ とする。このとき任意の $\lambda \in \Lambda$ に対し $A \in \mc{F}_\lambda$ であるので、
任意の $\lambda \in \Lambda$ に対し $\overline{A} \in \mc{F}_\lambda$
である。したがって $\overline{A} \in \mc{F}$ である。$A, B \in \mc{F}$ とする。このとき任意の $\lambda \in \Lambda$ に対し $A, B \in \mc{F}_\lambda$ であるので、
任意の $\lambda \in \Lambda$ に対し $A \cup B \in \mc{F}_\lambda$
である。したがって $A \cup B \in \mc{F}$ である。$\Lambda = \varnothing$ のときについて考えだすと
集合論の厄介な領域に踏み入っちゃいそうなので
ここでは避けてます($\bigcap \varnothing$ は宇宙だとかなんとか)
有限加法族を生成する
「~を含む最小の有限加法族」が定義できる
集合 $X$ の部分集合からなる集合 $\mc{F} \subseteq \mc{P}(X)$ に対し、$\mc{A}(\mc{F})$${}\subseteq \mc{P}(X)$ を
$X$ 上の有限加法族で $\mc{F}$ を包含するもの全ての共通部分
とする。すなわち $$\mc{A}(\mc{F}) = \bigcap_{ \begin{matrix} \text{${\mc{F}’}$ は $\mc{F} \subseteq \mc{F}’$ なる } \\ \text{$X$ の有限加法族} \end{matrix} } {\mc{F}’}$$ とする。問題18より、$\mc{A}(\mc{F})$ は $X$ の有限加法族である。$\mc{A}(\mc{F})$ を $\mc{F}$ から生成される $X$ 上の有限加法族と呼ぶ。
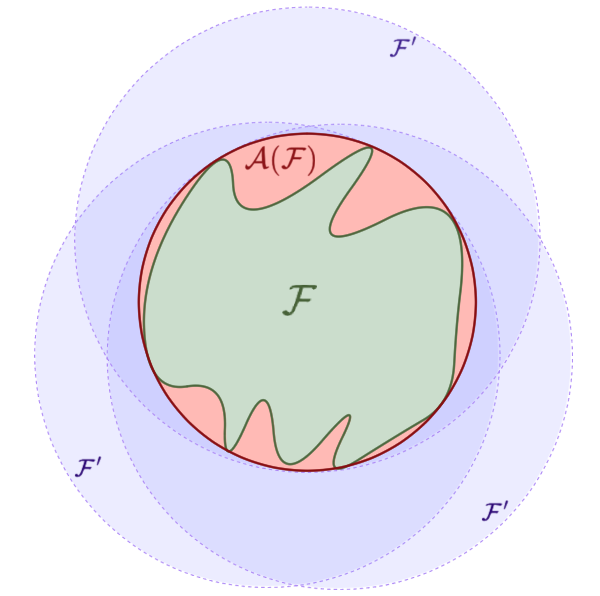
$\mc{F} \subseteq \mc{F}’$ なる任意の有限加法族 $\mc{F}’$ に対し $\mc{A}(\mc{F}) \subseteq \mc{F}’$ である。
$\mc{F} $ が集合 $X$ の有限加法族ならば $\mc{A}(\mc{F}) = \mc{F}$ である。
集合 $X = \cbr{1,2,3,4}$ に対し $$\mc{F} = \cbr{\cbr{1}, \cbr{1,2}}$$ とする。$\mc{F}$ から生成される $X$ の有限加法族 $\mc{A}(\mc{F})$ を求めよ。
$\mc{F}$ を包含する有限加法族 $\mc{F’}$ を任意に取る。まず $\mc{F} \subseteq \mc{F}’$ より $$\cbr{\cbr{1}, \cbr{1,2}} \subseteq \mc{F}’$$ である。また $\mc{F}’$ は補集合で閉じるので $$\cbr{\cbr{1}, \cbr{1,2}, \cbr{3,4},\cbr{2,3,4}} \subseteq \mc{F}’$$ である。更に $\mc{F}’$ は有限和で閉じるので $$\cbr{\cbr{1}, \cbr{1,2}, \cbr{3,4},\cbr{1,3,4}, \cbr{2,3,4}, \cbr{1,2,3,4}} \subseteq \mc{F}’$$ である。更に $\mc{F}’$ は補集合で閉じるので $$\cbr{\varnothing, \cbr{1}, \cbr{2}, \cbr{1,2}, \cbr{3,4}, \cbr{1,3,4}, \cbr{2,3,4}, \cbr{1,2,3,4}} \subseteq \mc{F}’$$ である。任意に取った $\mc{F}’$ に対してこの包含関係が成り立つので $$\cbr{\varnothing, \cbr{1}, \cbr{2}, \cbr{1,2}, \cbr{3,4}, \cbr{1,3,4}, \cbr{2,3,4}, \cbr{1,2,3,4}} \subseteq \mc{A}(\mc{F})$$ である。一方この左辺は非空で、補集合で閉じ、有限和で閉じるので有限加法族であり、また $\mc{F}$ を包含する。したがって逆向きの包含関係 $\supseteq$ も成り立つ。つまり $$\mc{A}(\mc{F}) = \cbr{\varnothing, \cbr{1}, \cbr{2}, \cbr{1,2}, \cbr{3,4}, \cbr{1,3,4}, \cbr{2,3,4}, \cbr{1,2,3,4}}$$ が求めるものである。
集合 $X$ の部分集合からなる集合 $\mc{F}, \mc{G} \subseteq \mc{P}(X)$ に対し、 $$\mc{F} \subseteq \mc{G} \implies \mc{A}(\mc{F}) \subseteq \mc{A}(\mc{G})$$ であることを示せ。
$\mc{G}$ を包含する有限加法族 $\mc{G}’$ を任意に取ると、 $$\mc{F} \subseteq \mc{G} \subseteq \mc{G}’$$ なので $\mc{G}’$ は $\mc{F}$ を包含する有限加法族。よって $$\mc{A}(\mc{F}) \subseteq \mc{G}’$$ である。任意に取った $\mc{G}’$ に対してこの包含関係が成り立つので、 $$\mc{A}(\mc{F}) \subseteq \mc{A}(\mc{G})$$ を得る。
集合 $X$ の部分集合からなる集合 $\mc{F}, \mc{G} \subseteq \mc{P}(X)$ に対し、 $$\mc{F} \subseteq \mc{G} \implies \mc{A}(\mc{F}) = \mc{A}(\mc{G})$$ は一般に成り立つか?
一般には成り立たない。実際 $X = \cbr{1,2,3}$ とし、 \begin{align} &\mc{F} = \cbr{\cbr{1}} && \mc{G} = \cbr{\cbr{1}, \cbr{2}} \end{align} とすると $\mc{F} \subseteq \mc{G}$ であるが、 \begin{align} \mc{A}(\mc{F}) &= \cbr{\varnothing, \cbr{1}, \cbr{2,3}, \cbr{1,2,3}} \\ \mc{A}(\mc{G}) &= \cbr{\varnothing, \cbr{1}, \cbr{2}, \cbr{3}, \cbr{1,2}, \cbr{1,3}, \cbr{2,3}, \cbr{1,2,3}} \end{align} となり、一致しない。
有限加法族は可算和で閉じるとは限らない
可算和で閉じない有限加法族の例を挙げよ。つまり集合 $X$ とその部分集合からなる集合 $\mc{F}$ で
「各 $n \in \NN$ に対し $A_n \in \mc{F}$」かつ $\ds\bigcup_{n \in \NN} {A_n} \not\in \mc{F}$
となる集合列 $\cbr{A_n}_{n \in \NN}$ が存在するものを作れ。$X = \NN$ とし、 $$\mc{F} = \iset{S \subseteq \NN}{\text{$S$ または $\overline{S}$ は有限集合}}$$ とするとこれは有限加法族(問題9)。$\mc{F}$ が可算和で閉じないことを示す。各 $n \in \NN$ に対し $A_n = \cbr{2n}$ とすると、これらは有限集合なので $A_n \in \mc{F}$ であるが、 $$\bigcup_{n \in \NN} A_n = \iset{2n}{n \in \NN} = \cbr{0,2,4,6,\ldots}$$ は無限集合であり、その補集合 $$\overline{\bigcup_{n \in \NN} A_n} = \iset{2n + 1}{n \in \NN} = \cbr{1,3,5,7,\ldots}$$ も無限集合である。したがって $\ds\bigcup_{n \in \NN} A_n \not\in \mc{F}$ となる。
有限加法族 $\mc{F}$ と写像 $f: \mc{F} \rightarrow [0,\infty)$ をせっかく作っても
各 $A_n$ の大きさが測れるからといって
$\ds\bigcup_{n} A_n$ の大きさが測れるとは限らない