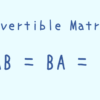正則行列と逆行列の理論の演習問題 18 問(解答付き)|線形代数学
正則行列・逆行列に関する演習問題で証明を書けるようになる。
- $\NN$ を非負整数全体の集合とする。
- 単位行列を $I$ と書く。$n$ 次であることを明示するときは $I_n$ と書くこともある。
- 零行列を $O$ と書く。
- 行列 $A$ の転置行列を $A^\top$ と表す。
- 第 $i$ 成分のみ $1$ でその他の成分が $0$ の列ベクトルを $e_i$ と書く。
以下、体 $K$ 上の行列を考える。
※「体」をご存じでない方は $K$ を $\RR$ や $\CC$ に置き換えてご覧ください。
理論的な演習問題をいろいろ解いてみよう
正則行列と逆行列
正方行列 $A$ が正則行列であるとは、 $$AB = BA = I$$ となる正方行列 $B$ が存在することをいう。
正方行列 $A$ に対し、
$AB = BA = I$ となる正方行列 $B$ は存在すればただ一つ
であることを示せ。正方行列 $B_1, B_2$ が $$AB_1 = B_1 A = I$$ $$AB_2 = B_2 A = I$$ を満たすとする。このとき $$B_1 = B_1 I = B_1 A B_2 = I B_2 = B_2$$ となるので、$AB = BA = I$ となる正方行列 $B$ は存在すればただ一つである。
正則行列 $A$ に対し、$AB = BA = I$ となる(ただ一つの)正方行列 $B$ を
$A$ の逆行列
と呼び、$A^{\minus 1}$ と書く。つまり $$AA^{\minus 1} = A^{\minus 1}A = I$$ である。$A^{\minus 1}$ の逆行列が $A$ に戻ることがわかります
正方行列 $A$ が正則行列ならば $A^{\minus 1}$ も正則行列であり
$(A^{\minus 1})^{\minus 1} = A$
である。正則行列と行列式
次の関係があります
正方行列 $A$ に対し、$A$ が正則行列であることと $\det A \neq 0$ であることは同値。
正方行列 $A, B$ に対し、
$AB = I$ $\quad$ ならば $\quad$ $BA = I$
であることを示せ。$AB = I$ となる正方行列 $A, B$ に対し $$\det A \det B = \det(AB) = \det I = 1$$ なので $\det A \neq 0$ である。よって $A$ は正則行列で、逆行列 $A^{\minus 1}$ が存在し、 $$BA = A^{\minus 1}ABA = A^{\minus 1}A = I$$
$AB = I$ となる $B$ の存在を示せば十分ってことだね
$BA = I$ から $AB = I$ が出てくるから
演習問題
単位行列 $I$ は正則行列であり $$I^{\minus 1} = I$$ であることを示せ。
$II = I$ なので $I$ は正則行列であり、$I^{\minus 1}$ である(問題2)。
正方零行列は正則行列でないことを示せ。
任意の正方行列 $B$ に対し $OB = O \neq I$ なので $O$ は正則行列でない。
$A$ が正則行列であればその転置行列 $A^\top$ も正則行列であり $$(A^\top)^{\minus 1} = (A^{\minus 1})^\top$$ であることを示せ。
$A$ が正則行列のとき、逆行列 $A^{\minus 1}$ が存在し、 $$A^\top(A^{\minus 1})^\top = (A^{\minus 1} A)^\top = I^\top = I$$ となる。よって $A^\top$ は正則行列であり、$A^\top$ の逆行列は $(A^{\minus 1})^\top$ である(問題2)。
三角行列 $A$ に対し
$A$ が正則行列 ${}\iff{}$ $A$ の対角成分に $0$ がない
が成り立つことを示せ。$A = (a_{i,j})_{i,j}$ と書くと \begin{align} \text{$A$ が正則行列} &\iff \det A \neq 0 \\&\iff a_{1,1} \cdots a_{n,n} \neq 0 \\&\iff \text{各 $i$ に対し $a_{i,i} \neq 0$} \\&\iff \text{$A$ の対角成分に $0$ がない} \end{align}
正則な上三角行列の逆行列は上三角行列であることを示せ。
※したがって問題5より、正則な下三角行列の逆行列も下三角行列。
「$n$ 次の正則な上三角行列の逆行列は上三角行列」を $n$ についての数学的帰納法で示す。
$1$ 次の正方行列は常に上三角行列なので、$n = 1$ のときは自明。
$A$ を $n + 1$ 次の正則な上三角行列とし、
$A = \pbr{ \begin{matrix} \ & \ & \ & * \\ \ & A_1 & \ & \vdots \\ \ & \ & \ & * \\ 0 & \cdots & 0 & a \end{matrix} }$ $\qquad$ $A^{\minus 1} = \pbr{ \begin{matrix} \ & \ & \ & * \\ \ & B_1 & \ & \vdots \\ \ & \ & \ & * \\ b_1 & \cdots & b_{n\minus 1} & * \end{matrix} }$
と書くことにする($A_1$ は $n$ 次上三角行列で $B_1$ は $n$ 次正方行列)。$AA^{\minus 1} = I_{n+1}$ なので $A_1 B_1 = I_n$ であり、したがって $A_1$ は正則で $B_1$ がその逆行列である。したがって帰納法の仮定より
$B_1$ は上三角行列
である。$AA^{\minus 1} = I_{n + 1}$ なので $AA^{\minus 1}$ の第 $(n, j)$ 成分($1 \leq j \leq n \minus 1$)は $0$ である。よって各 $j$ に対し $ab_j = 0$ であり、$A$ の正則性より $a \neq 0$ であるので
$b_1 = \cdots = b_{n \minus 1} = 0$
である。以上により $A^{\minus 1}$ が上三角行列であることがわかった。正方行列 $A$ が正則行列ならば、$c \in K \setminus \cbr{0}$ に対し $cA$ も正則行列であり $$(cA)^{\minus 1} = \dfrac{1}{c}A^{\minus 1}$$ であることを示せ。
$A$ が正則行列なので $A^{\minus 1}$ が存在し、 $$(cA)\pbr{\dfrac{1}{c}A^{\minus 1}} = \pbr{c \cdot \dfrac{1}{c}} A A^{\minus 1} = I$$ である。よって $cA$ は正則行列であり、$(cA)^{\minus 1} = \dfrac{1}{c}A^{\minus 1}$ である(問題2)。
正方行列 $A, B$ に対し、以下の各主張は正しいか?
正しくない。実際 $A = I$ および $B = \minus I$ とすると、$A$ も $B$ も正則行列だが、$A + B = O$ は正則行列ではない。
正しくない。実際 $A = B = I$ とすると、$A$ も $B$ も正則行列であり、$A + B = 2I$ も正則行列である。
正方行列 $A, B$ に対し、以下の各主張は正しいか?
正しくない。実際 $$A = \pbr{\begin{matrix} 1 & 0 \\ 0 & 1 \end{matrix}} \qquad B = \pbr{\begin{matrix} \minus 1 & 0 \\ 0 & 0 \end{matrix}} $$ とすると、$A$ は正則行列で $B$ は正則行列でないが、 $$A + B = \pbr{\begin{matrix} 0 & 0 \\ 0 & 1 \end{matrix}} $$ は正則行列でない。
正しくない。実際 $A = I$ および $B = O$ とすると、$A$ は正則行列であり $B$ は正則行列でないが、$A + B = I$ は正則行列である。
【参考】(1) でやりがち(?)な間違った解答
「$A$ が正則で $B$ が非正則ならば、$\det A \neq 0$ かつ $\det B = 0$ なので $$\det (A + B) = \det A + \det B = \det A \neq 0$$ となる。よって $A + B$ は正則行列である」
一般には成り立たないから この推論は誤り
正方行列 $A, B$ に対し、以下の各主張は正しいか?
正しくない。実際 $A = B = O$ とすると、$A$ も $B$ も正則行列ではなく、$A + B = O$ も正則行列でない。
正しくない。実際 $$A = \pbr{\begin{matrix} 1 & 0 \\ 0 & 0 \end{matrix}} \qquad B = \pbr{\begin{matrix} 0 & 0 \\ 0 & 1 \end{matrix}} $$ とすると $A$ も $B$ も正則行列でないが $$A + B = \pbr{\begin{matrix} 1 & 0 \\ 0 & 1 \end{matrix}} $$ は正則行列である。
正方行列 $A, B$ に対し、$A$ も $B$ も正則行列ならば $AB$ も正則行列であり $$(AB)^{\minus 1} = B^{\minus 1}A^{\minus 1}$$ であることを示せ。
$A$ も $B$ も正則行列なので $A^{\minus 1}$ と $B^{\minus 1}$ が存在し、 $$(AB) \pbr{B^{\minus 1}A^{\minus 1}} = AIA^{\minus 1} = AA^{\minus 1} = I$$ となる。よって $AB$ は正則で $(AB)^{\minus 1} = B^{\minus 1}A^{\minus 1}$ となる(問題2)。
正方行列 $A, B$ に対し、$A$ が正則行列でないならば、
$AB$ も $BA$ も正則行列でない
ことを示せ。もし $AB$ が正則行列で逆行列 $C$ を持つとすると $$ABC = I$$ となるが、これは $A$ が逆行列 $BC$ を持つことを意味するので矛盾。よって $AB$ は正則ではない。
もし $BA$ が正則行列で逆行列 $D$ を持つとすると $$DBA = I$$ となるが、これは $A$ が逆行列 $DB$ を持つことを意味するので矛盾。よって $BA$ は正則ではない。
いま $\det A = 0$ であるので、 $$\det (AB) = \det A \det B = 0$$ $$\det (BA) = \det B \det A = 0$$ となる。よって $AB$ も $BA$ も正則ではない。
正方行列 $A$ が冪零行列であるとは、
$A^m = O$ なる正整数 $m$ が存在する
ことをいう。冪零行列は正則行列でないことを示せ。
$A$ を冪零行列とし、$A^m = O$ なる最小の正整数 $m$ を取る。$m = 1$ のときは $A = O$ なので正則行列ではない。$m \geq 2$ のとき、仮に $A$ が正則行列で $$AB = I$$ となる行列 $B$ が存在すると、左から $A^{m \minus 1}$ を掛けることで $$O = A^{m \minus 1}$$ となるが、これは $m$ の最小性に反する。したがって $A$ は正則行列ではない。
$A$ を冪零行列とし、$A^m = O$ なる正整数 $m$ を取る。このとき $${\abs A}^m = \abs{A^m} = \abs{O} = 0$$ となるので $\abs A = 0$ である。よって $A$ は正則行列ではない。
$n$ 次正方行列 $A$ が冪零行列ならば $A^n = O$ であることを示せ。
$k$ を $A^k = O$ となる最小の正整数とする。$k = 1$ のときは $A = O$ なので自明。以下 $k \geq 2$ とする。 $A^{k \minus 1} \neq O$ なので、 $$A^{k \minus 1} v \neq \boldsymbol{0}$$ となる $v \neq \boldsymbol{0}$ が存在する(※1)。このとき $k$ 個のベクトル
$v, A v, A^2 v, \ldots, A^{k \minus 1} v$
の中に零ベクトルが存在しないことに注意(※2)。ここで $k \gt n$ を仮定すると、この $k$ 個のベクトルは一次従属となるので $$v = c_1 Av + c_2 A^2 v + \cdots + c_{k \minus 1} A^{k\minus 1}v$$ と表されるが、両辺に左から $A^{k\minus 1}$ を掛けると $A^{k \minus 1}v = \boldsymbol{0}$ となるので矛盾。よって $k \leq n$ であり、したがって $A^n = O$ である。
$A^{k \minus 1}$ の $(i,j)$ 成分が $0$ でないなら
$A^{k \minus 1}e_j \neq \boldsymbol{0}$
もし $A^i v = \boldsymbol{0}$ となる $i$ があれば
左から $A$ を何回か掛けると $A^{k \minus 1} v = \boldsymbol{0}$ になっちゃう
したがって $A$ を三角行列化すると
$B = P^{\minus 1}AP$ は対角成分がすべて $0$ で
よって $B^n = O$ となる
したがって $A^n = PB^nP^{\minus 1} = O$
という証明もアリ
$n$ 次正方行列 $A$ が冪零行列であるならば、各 $c \in K$ に対し $I + cA$ は正則行列で $$(I + cA)^{\minus 1} = I + (\minus cA) +\cdots + (\minus cA)^{n \minus 1}$$ であることを示せ。
$A^n = O$ であることに注意(問題15)すると \begin{align} &\phantom{ {}={} } (I + cA)(I + (\minus cA) + \cdots + (\minus cA)^{n \minus 1}) \\&= I + (\minus cA) + \cdots + (\minus cA)^{n \minus 1} \\&\qquad\qquad \minus (\minus cA) \minus (\minus cA)^2 \minus \cdots \minus (\minus cA)^n \\&= I \minus (\minus cA)^n \\&= I \end{align} であるので $I + cA$ は正則行列であり、 $$(I + cA)^{\minus 1} = I + (\minus cA) +\cdots + (\minus cA)^{n \minus 1}$$ である。
したがって $\det(I + cA) = 1$ となります
正方行列 $A, B$ がともに正則行列で $A^{\minus 1} + B^{\minus 1} = I$ ならば、$A \minus I$ も $B \minus I$ も正則行列で $$(A \minus I)^{\minus 1} = B \minus I$$ であることを示せ。
$A^{\minus 1} + B^{\minus 1} = I$ の左から $A$ を、右から $B$ を掛けると $$B + A = AB$$ となる。このとき $$(A \minus I)(B \minus I) = AB \minus A \minus B + I = I$$ となる。よって $A \minus I$ も $B \minus I$ も正則行列で $(A \minus I)^{\minus 1} = B \minus I$ となる。
$A^{\minus 1} + B^{\minus 1} = I$ の右から $A$ を、左から $B$ を掛けると $$B + A = BA$$ にもなるので $A$ と $B$ は可換($AB = BA$)
正則行列 $A$ が正方行列 $B_1, \ldots, B_k$ を用いて $$A = B_1 \cdots B_k$$ と表されるならば、$B_1, \ldots, B_k$ はいずれも正則で、各 $i$ に対し $$B_i^{\minus 1} = (B_{i + 1} \cdots B_{k}) A^{\minus 1} (B_1 \cdots B_{i \minus 1})$$ となることを示せ。
$k$ についての数学的帰納法で示す。$k = 1$ のときは自明。
正整数 $k$ に対し、正則行列 $A$ が $k+1$ 個の正方行列 $B_1, \ldots, B_k, B_{k+1}$ を用いて $$A = B_1 \cdots B_k B_{k + 1}$$ と表されているとする。$A$ が逆行列を持つので $$A^{\minus 1}B_1 \cdots B_k B_{k + 1} = A^{\minus 1} A = I$$ となり、よって $B_{k + 1}$ は正則で $$B_{k + 1}^{\minus 1} = A^{\minus 1}B_1 \cdots B_k$$ となる。更にこのとき正則行列 $AB_{k + 1}^{\minus 1}$ が $k$ 個の正方行列 $B_1, \ldots, B_k$ の積で表される。したがって帰納法の仮定より $B_1, \ldots, B_k$ はいずれも正則で、各 $i$ に対し \begin{align} B_i^{\minus 1} &= (B_{i + 1} \cdots B_{k}) (AB_{k + 1}^{\minus 1})^{\minus 1} (B_1 \cdots B_{i \minus 1}) \\&=(B_{i + 1} \cdots B_{k} B_{k+1}) A^{\minus 1} (B_1 \cdots B_{i \minus 1}) \end{align} となり、証明が終わる。