行列式の計算の演習問題 12 問(解答付き)|線形代数学
行列式の計算問題を解けるようになる。
たくさん解こう
復習用の例題
例題で簡単に復習しよう
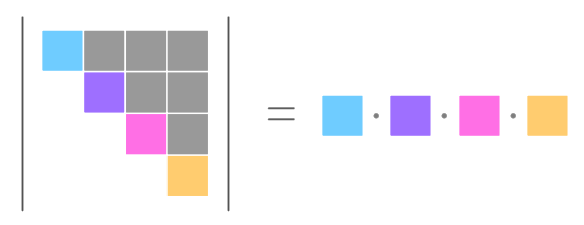
$$\abs{ \begin{matrix} 3 & 9 & \minus 4 & 12 \\ 0 & 1 & 8 & 4 \\ 0 & 0 & \minus 1 & 7 \\ 0 & 0 & 0 & 10 \end{matrix} } = 3 \cdot 1 \cdot (\minus 1) \cdot 10 = \minus 30 $$
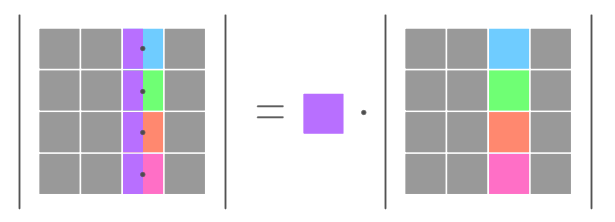
行列式が $(\minus 1)$ 倍になる
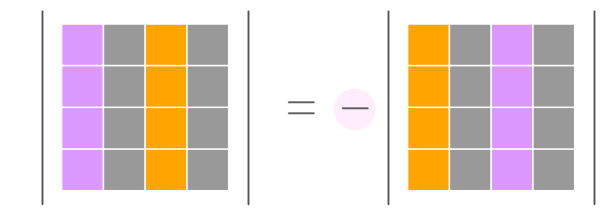
\begin{align} &\phantom{ {}={} }\abs{ \begin{matrix} \minus 1 & 1 & 6 & 8 \\ 9 & 1 & 0 & 9 \\ 2 & 0 & 0 & 4 \\ 0 & 0 & 0 & 3 \end{matrix} } \\ &&& \text{↓ 第 $1$ 列と第 $3$ 列を入れ替え} \\ &= \minus \abs{ \begin{matrix} 6 & 1 & \minus 1 & 8 \\ 0 & 1 & 9 & 9 \\ 0 & 0 & 2 & 4 \\ 0 & 0 & 0 & 3 \end{matrix} } \\ &&& \text{↓ 三角行列の行列式} \\ &= \minus 6 \cdot 1 \cdot 2 \cdot 3 \\ \\ &= \minus 36 \end{align}
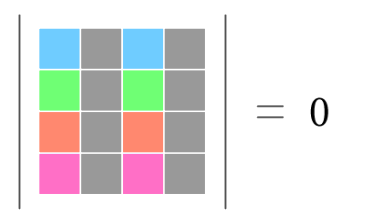
\begin{align} &\phantom{ {}={} }\abs{ \begin{matrix} 7 & 0 & 7 & 6 \\ 3 & 8 & 3 & 5 \\ 1 & 9 & 1 & 2 \\ 2 & 4 & 2 & 1 \end{matrix} } = 0 & \text{第 $1$ 列と第 $3$ 列が等しい} \end{align}
\begin{align} &\phantom{ {}={} }\abs{ \begin{matrix} 3 & 4 & 6 & 2 \\ 2 & 4 & 9 & 3 \\ 4 & 1 & \minus 3 & \minus 1 \\ 3 & 1 & 3 & 1 \end{matrix} } \\ &&& \text{↓ 第 $3$ 列から因数 $3$ を外へ} \\ &=3 \cdot \abs{ \begin{matrix} 3 & 4 & 2 & 2 \\ 2 & 4 & 3 & 3 \\ 4 & 1 & \minus 1 & \minus 1 \\ 3 & 1 & 1 & 1 \end{matrix} } \\ &&& \text{↓ 第 $3$ 列と第 $4$ 列が等しい} \\ &= 0 \end{align}
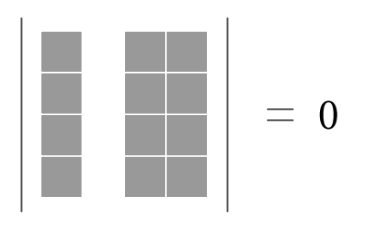
\begin{align} & \abs{ \begin{matrix} 2 & 0 & 5 & 2 \\ 9 & 0 & 7 & 2 \\ 1 & 0 & 4 & 3 \\ 3 & 0 & 3 & 0 \end{matrix} } =0 &&& \text{第 $2$ 列が $0$} \end{align}
行列式は変わらない
\begin{align} & \phantom{ {}={} }\abs{ \begin{matrix} 3 & 1 & 5 & 2 \\ 0 & 1 & 2 & 1 \\ 0 & 1 & 1 & 1 \\ 0 & 0 & 2 & 1 \end{matrix} } \\ &&&\text{↓ 第 $2$ 行の $(\minus 1)$ 倍を第 $3$ 行に加算} \\ &= \abs{ \begin{matrix} 3 & 1 & 5 & 2 \\ 0 & 1 & 2 & 1 \\ 0 & 0 & \minus 1 & 0 \\ 0 & 0 & 2 & 1 \end{matrix} } \\ &&&\text{↓ 第 $3$ 行の $2$ 倍を第 $4$ 行に加算} \\ &= \abs{ \begin{matrix} 3 & 1 & 5 & 2 \\ 0 & 1 & 2 & 1 \\ 0 & 0 & \minus 1 & 0 \\ 0 & 0 & 0 & 1 \end{matrix} } \\ &&&\text{↓ 三角行列の行列式} \\ &= 3 \cdot 1 \cdot (\minus 1) \cdot 1 \\ \\ &= \minus 3 \end{align}
$(i,j)$ 成分の値と $(i,j)$ 余因子を掛けたものを
すべて足し合わせたものが 元の行列の行列式
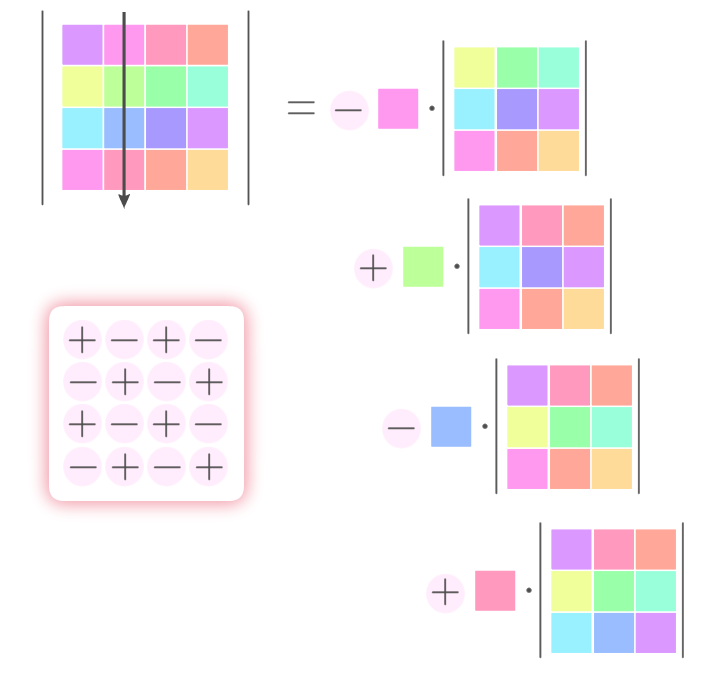
\begin{align} & \phantom{ {}={} }\abs{ \begin{matrix} 1 & 0 & 0 & 6 \\ 0 & 2 & 3 & 0 \\ 5 & 3 & 0 & 1 \\ 0 & 0 & 5 & 2 \end{matrix} } \\ \\ & \qquad \text{↓ 第 $2$ 列に沿って余因子展開} \\ \\ &= 0 + (\minus 1)^{2 + 2} \cdot 2 \abs{ \begin{matrix} 1 & 0 & 6 \\ 5 & 0 & 1 \\ 0 & 5 & 2 \end{matrix} } + (\minus 1)^{3 + 2} \cdot 3 \abs{ \begin{matrix} 1 & 0 & 6 \\ 0 & 3 & 0 \\ 0 & 5 & 2 \end{matrix} } + 0 \\ \\ & \qquad \text{↓ 第 $2$ 列に沿って余因子展開} \qquad \text{↓ 第 $1$ 列に沿って余因子展開} \\ \\ &= 2 \cdot \pbr{0 + 0 + (\minus 1)^{3 + 2} \cdot 5 \cdot \abs{ \begin{matrix} 1 & 6 \\ 5 & 1 \end{matrix} } } \\&\qquad \qquad \qquad \minus 3 \cdot \pbr{ (\minus 1)^{1+1} \cdot 1 \cdot \abs{ \begin{matrix} 3 & 0 \\ 5 & 2 \end{matrix} } + 0 + 0} \\ \\ &= \minus 10 (1 \minus 30) \minus 3 (6 \minus 0) \\ \\ &= 272 \end{align}
あらかじめ別の操作で
余因子展開したい列(行)で
$0$ の成分を増やしておくのがオススメ
$(3,1)$ 成分を $0$ にしてから
第 $1$ 列に沿って余因子展開するとかかな
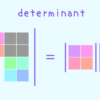
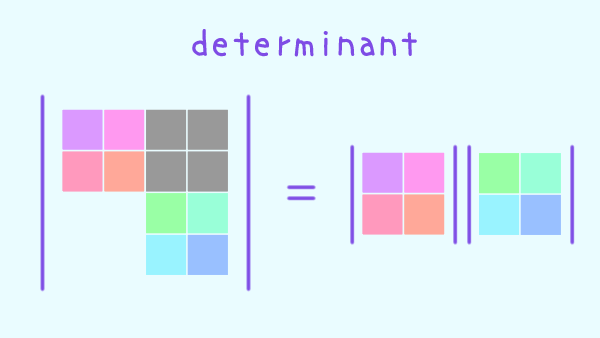
左下が全て $0$ なら
元の行列式は 左上の行列式と右下の行列式の積
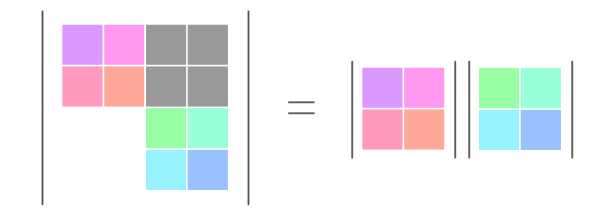
\begin{align} & \phantom{ {}={} }\abs{ \begin{matrix} 2 & 0 & 9 & 1 \\ 3 & 2 & 5 & 3 \\ 0 & 1 & 1 & 1 \\ 0 & 1 & 5 & 1 \end{matrix} } \\ &&&\text{↓ 第 $4$ 列の $(\minus 1)$ 倍を第 $2$ 列に加算} \\ &= \abs{ \begin{matrix} 2 & \minus 1 & 9 & 1 \\ 3 & \minus 1 & 5 & 3 \\ 0 & 0 & 1 & 1 \\ 0 & 0 & 5 & 1 \end{matrix} } \\ &&&\text{↓ 左上と右下の行列に分解} \\ &= \abs{ \begin{matrix} 2 & \minus 1 \\ 3 & \minus 1 \end{matrix} } \abs{ \begin{matrix} 1 & 1 \\ 5 & 1 \end{matrix} } \\ \\ &= (\minus 2 \minus (\minus 3)) \cdot (1 \minus 5) \\ \\ &= \minus 4 \end{align}
演習問題
次の行列の行列式を計算せよ。 $$ A = \pbr{ \begin{matrix} 0 & 3 & \minus 4 \\ 1 & 0 & 2 \\ \minus 1 & 0 & 2 \end{matrix} } $$
\begin{align} \det A &= 0 \cdot 0 \cdot 2 + 3 \cdot 2 \cdot (\minus 1) + (\minus 4) \cdot 1 \cdot 0 \\&\qquad \minus 0 \cdot 2 \cdot 0 \minus 3 \cdot 1 \cdot 2 \minus (\minus 4) \cdot 0 \cdot (\minus 1) \\&= \minus 6 \minus 6 \\&= \minus 12 \end{align}
\begin{align} \det A &=\abs{ \begin{matrix} 0 & 3 & \minus 4 \\ 1 & 0 & 2 \\ \minus 1 & 0 & 2 \end{matrix} } \\ &&&\text{↓ 第 $1$ 列と第 $2$ 列を入れ替え} \\ &= \minus \abs { \begin{matrix} 3 & 0 & \minus 4 \\ 0 & 1 & 2 \\ 0 & \minus 1 & 2 \end{matrix} } \\ &&&\text{↓ 第 $2$ 行の $1$ 倍を第 $3$ 行に加算} \\ &= \minus \abs { \begin{matrix} 3 & 0 & \minus 4 \\ 0 & 1 & 2 \\ 0 & 0 & 4 \end{matrix} } \\ &&&\text{↓ 三角行列の行列式} \\ &= \minus (3 \cdot 1 \cdot 4) \\\\ &= \minus 12 \end{align}
\begin{align} \det A &=\abs{ \begin{matrix} 0 & 3 & \minus 4 \\ 1 & 0 & 2 \\ \minus 1 & 0 & 2 \end{matrix} } \\ &&&\text{↓ 第 $1$ 列と第 $2$ 列を入れ替え} \\ &= \minus \abs { \begin{matrix} 3 & 0 & \minus 4 \\ 0 & 1 & 2 \\ 0 & \minus 1 & 2 \end{matrix} } \\ &&&\text{↓ 左上と右下の行列に分解} \\ &= \minus \abs{3} \abs { \begin{matrix} 1 & 2 \\ \minus 1 & 2 \end{matrix} } \\\\ &= \minus 3(2 \minus (\minus 2)) \\\\ &= \minus 12 \end{align}
\begin{align} \det A &=\abs{ \begin{matrix} 0 & 3 & \minus 4 \\ 1 & 0 & 2 \\ \minus 1 & 0 & 2 \end{matrix} } \\ &&&\text{↓ 第 $2$ 列に沿って余因子展開} \\ &= (-1)^{1 + 2} \cdot 3 \abs { \begin{matrix} 1 & 2 \\ \minus 1 & 2 \end{matrix} } + 0 + 0 \\\\ &=\minus 3 (2 \minus (\minus 2)) \\\\ &= \minus 12 \end{align}
\begin{align} \det A &=\abs{ \begin{matrix} 0 & 3 & \minus 4 \\ 1 & 0 & 2 \\ \minus 1 & 0 & 2 \end{matrix} } \\ &&&\text{↓ 第 $1$ 列に沿って余因子展開} \\ &= 0 + (-1)^{2 + 1} \cdot 1 \abs { \begin{matrix} 3 & \minus 4 \\ 0 & 2 \end{matrix} } \\&\qquad + (-1)^{3 + 1} \cdot (\minus 1) \abs { \begin{matrix} 3 & \minus 4 \\ 0 & 2 \end{matrix} } \\\\ &=\minus (6 \minus 0) \minus (6 \minus 0) \\\\ &= \minus 12 \end{align}
次の行列の行列式を計算せよ。 $$ A = \pbr{ \begin{matrix} 0 & 0 & 0 & 1 \\ 0 & 0 & 2 & 0 \\ 0 & 3 & 0 & 0 \\ 4 & 0 & 0 & 0 \end{matrix} } $$
\begin{align} \det A &= \abs{ \begin{matrix} 0 & 0 & 0 & 1 \\ 0 & 0 & 2 & 0 \\ 0 & 3 & 0 & 0 \\ 4 & 0 & 0 & 0 \end{matrix} } \\ &&&\text{↓ 第 $1$ 列と第 $4$ 列を入れ替え} \\ &= \minus\abs{ \begin{matrix} 1 & 0 & 0 & 0 \\ 0 & 0 & 2 & 0 \\ 0 & 3 & 0 & 0 \\ 0 & 0 & 0 & 4 \end{matrix} } \\ &&&\text{↓ 第 $2$ 列と第 $3$ 列を入れ替え} \\ &= \abs{ \begin{matrix} 1 & 0 & 0 & 0 \\ 0 & 2 & 0 & 0 \\ 0 & 0 & 3 & 0 \\ 0 & 0 & 0 & 4 \end{matrix} } \\ &&&\text{↓ 三角行列の行列式} \\ &= 1 \cdot 2 \cdot 3 \cdot 4 \\\\ &= 24 \end{align}
\begin{align} \det A &= \abs{ \begin{matrix} 0 & 0 & 0 & 1 \\ 0 & 0 & 2 & 0 \\ 0 & 3 & 0 & 0 \\ 4 & 0 & 0 & 0 \end{matrix} } \\ &&&\text{↓ 第 $1$ 列に沿って余因子展開} \\ &= (\minus 1)^{4+1}\cdot 4 \cdot \abs{ \begin{matrix} 0 & 0 & 1 \\ 0 & 2 & 0 \\ 3 & 0 & 0 \end{matrix} } \\ &&&\text{↓ 第 $1$ 列に沿って余因子展開} \\ &= (\minus 4) \cdot (\minus 1)^{3+1} \cdot 3 \cdot \abs{ \begin{matrix} 0 & 1 \\ 2 & 0 \end{matrix} } \\ &&&\text{↓ 第 $1$ 列に沿って余因子展開} \\ &= (\minus 12) \cdot (\minus 1)^{2+1} \cdot 2 \cdot \abs{ \begin{matrix} 1 \end{matrix} } \\\\ &= 24 \end{align}
次の行列の行列式を計算せよ。 $$ A = \pbr{ \begin{matrix} 1 & 2 & 3 & 4 \\ 5 & 6 & 7 & 8 \\ 9 & 10 & 11 & 12 \\ 13 & 14 & 15 & 16 \end{matrix} } $$
\begin{align} \det A &= \abs{ \begin{matrix} 1 & 2 & 3 & 4 \\ 5 & 6 & 7 & 8 \\ 9 & 10 & 11 & 12 \\ 13 & 14 & 15 & 16 \end{matrix} } \\ &&&\text{↓ 第 $1$ 行の $(\minus 1)$ 倍を第 $2$ 行に加算} \\ &= \abs{ \begin{matrix} 1 & 2 & 3 & 4 \\ 4 & 4 & 4 & 4 \\ 9 & 10 & 11 & 12 \\ 13 & 14 & 15 & 16 \end{matrix} } \\ &&&\text{↓ 第 $2$ 行の $(\minus 1)$ 倍を第 $3$ 行に加算} \\ &= \abs{ \begin{matrix} 1 & 2 & 3 & 4 \\ 4 & 4 & 4 & 4 \\ 8 & 8 & 8 & 8 \\ 13 & 14 & 15 & 16 \end{matrix} } \\ &&&\text{↓ 第 $3$ 行の因数 $2$ を外へ} \\ &= 2 \cdot \abs{ \begin{matrix} 1 & 2 & 3 & 4 \\ 4 & 4 & 4 & 4 \\ 4 & 4 & 4 & 4 \\ 13 & 14 & 15 & 16 \end{matrix} } \\ &&&\text{↓ 第 $2$ 行と第 $3$ 行が等しい} \\ &= 0 \end{align}
次の行列の行列式を計算せよ。 $$ A = \pbr{ \begin{matrix} 1 & \minus 1 & 1 & \minus 1 \\ 1 & \minus 2 & 1 & \minus 2 \\ 1 & \minus 2 & 2 & \minus 1 \\ 1 & \minus 2 & 2 & \minus 2 \end{matrix} } $$
\begin{align} \det A &= \abs{ \begin{matrix} 1 & \minus 1 & 1 & \minus 1 \\ 1 & \minus 2 & 1 & \minus 2 \\ 1 & \minus 2 & 2 & \minus 1 \\ 1 & \minus 2 & 2 & \minus 2 \end{matrix} } \\ &&&\text{↓ 第 $2$ 行の $(\minus 1)$ 倍を第 $3$ 行に加算} \\ &= \abs{ \begin{matrix} 1 & \minus 1 & 1 & \minus 1 \\ 1 & \minus 2 & 1 & \minus 2 \\ 0 & 0 & 1 & 1 \\ 1 & \minus 2 & 2 & \minus 2 \end{matrix} } \\ &&&\text{↓ 第 $2$ 行の $(\minus 1)$ 倍を第 $4$ 行に加算} \\ &= \abs{ \begin{matrix} 1 & \minus 1 & 1 & \minus 1 \\ 1 & \minus 2 & 1 & \minus 2 \\ 0 & 0 & 1 & 1 \\ 0 & 0 & 1 & 0 \end{matrix} } \\ &&&\text{↓ 左上と右下の行列に分解} \\ &= \abs{ \begin{matrix} 1 & \minus 1 \\ 1 & \minus 2 \end{matrix} } \abs{ \begin{matrix} 1 & 1 \\ 1 & 0 \end{matrix} } \\ \\ &= (\minus 2 \minus (\minus 1)) (0 \minus 1) \\ \\ &= 1 \end{align}
\begin{align} \det A &= \abs{ \begin{matrix} 1 & \minus 1 & 1 & \minus 1 \\ 1 & \minus 2 & 1 & \minus 2 \\ 1 & \minus 2 & 2 & \minus 1 \\ 1 & \minus 2 & 2 & \minus 2 \end{matrix} } \\ &&&\text{↓ 第 $1$ 列の $2$ 倍を第 $2$ 列に加算} \\ &= \abs{ \begin{matrix} 1 & 1 & 1 & \minus 1 \\ 1 & 0 & 1 & \minus 2 \\ 1 & 0 & 2 & \minus 1 \\ 1 & 0 & 2 & \minus 2 \end{matrix} } \\ &&&\text{↓ 第 $2$ 列に沿って余因子展開} \\ &= (\minus 1) \cdot 1 \cdot \abs{ \begin{matrix} 1 & 1 & \minus 2 \\ 1 & 2 & \minus 1 \\ 1 & 2 & \minus 2 \end{matrix} } \\ &&&\text{↓ 第 $1$ 列の $(\minus 2)$ 倍を第 $2$ 列に加算} \\ &= \minus \abs{ \begin{matrix} 1 & \minus 1 & \minus 2 \\ 1 & 0 & \minus 1 \\ 1 & 0 & \minus 2 \end{matrix} } \\ &&&\text{↓ 第 $2$ 列に沿って余因子展開} \\ &= \minus (\minus 1)^{1 + 2} \cdot (\minus 1) \cdot \abs{ \begin{matrix} 1 & \minus 1 \\ 1 & \minus 2 \end{matrix} } \\ \\ &= \minus (\minus 2 \minus (\minus 1)) \\ \\ &= 1 \end{align}
次の行列の行列式を計算せよ。 $$ A = \pbr{ \begin{matrix} 4 & \minus 1 & \minus 2 \\ 0 & 5 & \minus 3 \\ 2 & 1 & 2 \end{matrix} } $$
\begin{align} \det A &= \abs{ \begin{matrix} 4 & \minus 1 & \minus 2 \\ 0 & 5 & \minus 3 \\ 2 & 1 & 2 \end{matrix} } \\ &&&\text{↓ 第 $1$ 行の $1$ 倍を第 $3$ 行に加算} \\ &= \abs{ \begin{matrix} 4 & \minus 1 & \minus 2 \\ 0 & 5 & \minus 3 \\ 6 & 0 & 0 \end{matrix} } \\ &&&\text{↓ 第 $3$ 行に沿って余因子展開} \\ &= (\minus 1)^{3 + 1} \cdot 6 \cdot \abs{ \begin{matrix} \minus 1 & \minus 2 \\ 5 & \minus 3 \end{matrix} } \\ \\ &= 6 \cdot (3 \minus (\minus 10)) \\ \\ &=78 \end{align}
\begin{align} \det A &= \abs{ \begin{matrix} 4 & \minus 1 & \minus 2 \\ 0 & 5 & \minus 3 \\ 2 & 1 & 2 \end{matrix} } \\ &&&\text{↓ 第 $1$ 行の $\pbr{\minus \dfrac{1}{2}}$ 倍を第 $3$ 行に加算} \\ &= \abs{ \begin{matrix} 4 & \minus 1 & \minus 2 \\ 0 & 5 & \minus 3 \\ 0 & \dfrac{3}{2} & 3 \end{matrix} } \\ &&&\text{↓ 第 $2$ 行の $\pbr{\minus \dfrac{3}{10}}$ 倍を第 $3$ 行に加算} \\ &= \abs{ \begin{matrix} 4 & \minus 1 & \minus 2 \\ 0 & 5 & \minus 3 \\ 0 & 0 & \dfrac{39}{10} \end{matrix} } \\ \\ &= 4 \cdot 5 \cdot \dfrac{39}{10} \\ &=78 \end{align}
次の行列の行列式を計算せよ。 $$ A = \pbr{ \begin{matrix} 0 & 0 & 1 & 1 & 1 \\ 0 & 1 & 1 & 1 & 0 \\ 1 & 1 & 1 & 0 & 0 \\ 1 & 1 & 0 & 0 & 1 \\ 1 & 0 & 0 & 1 & 1 \end{matrix} } $$
\begin{align} \det A &= \abs{ \begin{matrix} 0 & 0 & 1 & 1 & 1 \\ 0 & 1 & 1 & 1 & 0 \\ 1 & 1 & 1 & 0 & 0 \\ 1 & 1 & 0 & 0 & 1 \\ 1 & 0 & 0 & 1 & 1 \end{matrix} } \\ &&&\text{↓ 第 $3$ 行の $(\minus 1)$ 倍を} \\ &&&\quad\text{第 $4$ 行と第 $5$ 行に加算} \\ &= \abs{ \begin{matrix} 0 & 0 & 1 & 1 & 1 \\ 0 & 1 & 1 & 1 & 0 \\ 1 & 1 & 1 & 0 & 0 \\ 0 & 0 & \minus 1 & 0 & 1 \\ 0 & \minus 1 & \minus 1 & 1 & 1 \end{matrix} } \\ &&&\text{↓ 第 $1$ 列に沿って余因子展開} \\ &= (\minus 1)^{3 + 1} \cdot 1 \cdot \abs{ \begin{matrix} 0 & 1 & 1 & 1 \\ 1 & 1 & 1 & 0 \\ 0 & \minus 1 & 0 & 1 \\ \minus 1 & \minus 1 & 1 & 1 \end{matrix} } \\ &&&\text{↓ 第 $2$ 行の $1$ 倍を} \\ &&&\quad\text{第 $4$ 行に加算} \\ &= \abs{ \begin{matrix} 0 & 1 & 1 & 1 \\ 1 & 1 & 1 & 0 \\ 0 & \minus 1 & 0 & 1 \\ 0 & 0 & 2 & 1 \end{matrix} } \\ &&&\text{↓ 第 $1$ 列に沿って余因子展開} \\ &= (\minus 1)^{2 + 1} \cdot 1 \cdot \abs{ \begin{matrix} 1 & 1 & 1 \\ \minus 1 & 0 & 1 \\ 0 & 2 & 1 \end{matrix} } \\ &&&\text{↓ 第 $1$ 行の $1$ 倍を} \\ &&&\quad\text{第 $2$ 行に加算} \\ &= (\minus 1) \cdot \abs{ \begin{matrix} 1 & 1 & 1 \\ 0 & 1 & 2 \\ 0 & 2 & 1 \end{matrix} } \\ &&&\text{↓ 第 $1$ 列に沿って余因子展開} \\ &= (\minus 1) \cdot (\minus 1)^{1 + 1} \cdot 1 \cdot \abs{ \begin{matrix} 1 & 2 \\ 2 & 1 \end{matrix} } \\ \\ &= (\minus 1) (1 \minus 4) \\ \\ &= 3 \end{align}
実数 $a$ に対し次の行列の行列式を計算せよ。 $$ A = \pbr{ \begin{matrix} a \minus 1 & a + 1 & a \\ a + 1 & a & a \minus 1 \\ a & a \minus 1 & a + 1 \end{matrix} } $$
\begin{align} \det A &= \abs{ \begin{matrix} a \minus 1 & a + 1 & a \\ a + 1 & a & a \minus 1 \\ a & a \minus 1 & a + 1 \end{matrix} } \\ &&&\text{↓ 第 $3$ 行の $(\minus 1)$ 倍を} \\ &&&\quad\text{第 $1$ 行と第 $2$ 行に加算} \\ &= \abs{ \begin{matrix} \minus 1 & 2 & \minus 1 \\ 1 & 1 & \minus 2 \\ a & a \minus 1 & a + 1 \end{matrix} } \\ &&&\text{↓ 第 $2$ 行の $1$ 倍を} \\ &&&\quad\text{第 $1$ 行に加算} \\ &= \abs{ \begin{matrix} 0 & 3 & \minus 3 \\ 1 & 1 & \minus 2 \\ a & a \minus 1 & a + 1 \end{matrix} } \\ &&&\text{↓ 第 $2$ 行の $(\minus a)$ 倍を} \\ &&&\quad\text{第 $3$ 行に加算} \\ &= \abs{ \begin{matrix} 0 & 3 & \minus 3 \\ 1 & 1 & \minus 2 \\ 0 & \minus 1 & 3a + 1 \end{matrix} } \\ &&&\text{↓ 第 $1$ 列に沿って余因子展開} \\ &= (\minus 1)^{2 + 1} \cdot 1 \cdot \abs{ \begin{matrix} 3 & \minus 3 \\ \minus 1 & 3a + 1 \end{matrix} } \\ \\ &= \minus ((9a + 3) \minus 3) \\ \\ &= \minus 9a \end{align}
実数 $a$ に対し次の行列の行列式を計算せよ。 $$ A = \pbr{ \begin{matrix} 1 & a & a^2 & a^3 \\ a & a^2 & a^3 & a^4 \\ a^2 & a^3 & a^4 & a^5 \\ a^3 & a^4 & a^5 & a^6 \end{matrix} } $$
\begin{align} \det A &= \abs{ \begin{matrix} 1 & a & a^2 & a^3 \\ a & a^2 & a^3 & a^4 \\ a^2 & a^3 & a^4 & a^5 \\ a^3 & a^4 & a^5 & a^6 \end{matrix} } \\ &&&\text{↓ 第 $1$ 行の $(\minus a)$ 倍を} \\ &&&\quad\text{第 $2$ 行に加算} \\ &= \abs{ \begin{matrix} 1 & a & a^2 & a^3 \\ 0 & 0 & 0 & 0 \\ a^2 & a^3 & a^4 & a^5 \\ a^3 & a^4 & a^5 & a^6 \end{matrix} } \\ &&&\text{↓ 第 $2$ 行がすべて $0$} \\ &= 0 \end{align}
実数 $a$ に対し次の行列の行列式を計算せよ。 $$ A = \pbr{ \begin{matrix} 1 & a & a^2 \\ a & a^2 & a^4 \\ a^2 & a^4 & a^8 \end{matrix} } $$
\begin{align} \det A &= \abs{ \begin{matrix} 1 & a & a^2 \\ a & a^2 & a^4 \\ a^2 & a^4 & a^8 \end{matrix} } \\ &&&\text{↓ 第 $1$ 行の $(\minus a)$ 倍を第 $2$ 行に加算} \\ &= \abs{ \begin{matrix} 1 & a & a^2 \\ 0 & 0 & a^4 \minus a^3 \\ a^2 & a^4 & a^8 \end{matrix} } \\ &&&\text{↓ 第 $1$ 行の $(\minus a^2)$ 倍を第 $3$ 行に加算} \\ &= \abs{ \begin{matrix} 1 & a & a^2 \\ 0 & 0 & a^4 \minus a^3 \\ 0 & a^4 \minus a^3 & a^8 \minus a^4 \end{matrix} } \\ &&&\text{↓ 第 $1$ 列に沿って余因子展開} \\ &= \abs{ \begin{matrix} 0 & a^4 \minus a^3 \\ a^4 \minus a^3 & a^8 \minus a^4 \end{matrix} } \\ &&&\text{↓ 第 $2$ 行の $(\minus a^2)$ 倍を第 $3$ 行に加算} \\ &= \minus (a^4 \minus a^3)^2 \\ \\ &= \minus a^6(a \minus 1)^2 \end{align}
実数 $a$ に対し次の行列の行列式を計算せよ。 $$ A = \pbr{ \begin{matrix} a & 2a+1 & 3a+2 & 4a + 3 \\ 2a+1 & 3a+2 & 4a + 3 & 3a+4 \\ 3a+2 & 4a + 3 & 3a+4 & 2a+5 \\ 4a + 3 & 3a+4 & 2a+5 & a+6 \end{matrix} } $$
\begin{align} \det A &= \abs{ \begin{matrix} a & 2a+1 & 3a+2 & 4a + 3 \\ 2a+1 & 3a+2 & 4a + 3 & 3a+4 \\ 3a+2 & 4a + 3 & 3a+4 & 2a+5 \\ 4a + 3 & 3a+4 & 2a+5 & a+6 \end{matrix} } \\ \\ &\qquad\qquad\text{↓ 第 $1$ 行の $(\minus 2)$ 倍を第 $2$ 行に加算} \\ \\ &= \abs{ \begin{matrix} a & 2a+1 & 3a+2 & 4a + 3 \\ 1 & \minus a & \minus 2a \minus 1 & \minus 5a \minus 2 \\ 3a+2 & 4a + 3 & 3a+4 & 2a+5 \\ 4a + 3 & 3a+4 & 2a+5 & a+6 \end{matrix} } \\ \\ &\qquad\qquad\text{↓ 第 $1$ 行の $(\minus 3)$ 倍を第 $3$ 行に加算} \\ \\ &= \abs{ \begin{matrix} a & 2a+1 & 3a+2 & 4a + 3 \\ 1 & \minus a & \minus 2a \minus 1 & \minus 5a \minus 2 \\ 2 & \minus 2a & \minus 6a \minus 2 & \minus 10a \minus 4 \\ 4a + 3 & 3a+4 & 2a+5 & a+6 \end{matrix} } \\ \\ &\qquad\qquad\text{↓ 第 $1$ 行の $(\minus 4)$ 倍を第 $4$ 行に加算} \\ \\ &= \abs{ \begin{matrix} a & 2a+1 & 3a+2 & 4a + 3 \\ 1 & \minus a & \minus 2a \minus 1 & \minus 5a \minus 2 \\ 2 & \minus 2a & \minus 6a \minus 2 & \minus 10a \minus 4 \\ 3 & \minus 5a & \minus 10a \minus 3 & \minus 15a \minus 6 \end{matrix} } \\ \\ &\qquad\qquad\text{↓ 第 $2$ 行の $(\minus a)$ 倍を第 $1$ 行に加算} \\ \\ &= \abs{ \begin{matrix} 0 & a^2 + 2a+1 & 2a^2 + 4a+2 & 5a^2 + 6a + 3 \\ 1 & \minus a & \minus 2a \minus 1 & \minus 5a \minus 2 \\ 2 & \minus 2a & \minus 6a \minus 2 & \minus 10a \minus 4 \\ 3 & \minus 5a & \minus 10a \minus 3 & \minus 15a \minus 6 \end{matrix} } \\ \\ &\qquad\qquad\text{↓ 第 $2$ 行の $(\minus 2)$ 倍を第 $3$ 行に加算} \\ \\ &= \abs{ \begin{matrix} 0 & a^2 + 2a+1 & 2a^2 + 4a+2 & 5a^2 + 6a + 3 \\ 1 & \minus a & \minus 2a \minus 1 & \minus 5a \minus 2 \\ 0 & 0 & \minus 2a & 0 \\ 3 & \minus 5a & \minus 10a \minus 3 & \minus 15a \minus 6 \end{matrix} } \\ \\ &\qquad\qquad\text{↓ 第 $2$ 行の $(\minus 3)$ 倍を第 $4$ 行に加算} \\ \\ &= \abs{ \begin{matrix} 0 & a^2 + 2a+1 & 2a^2 + 4a+2 & 5a^2 + 6a + 3 \\ 1 & \minus a & \minus 2a \minus 1 & \minus 5a \minus 2 \\ 0 & 0 & \minus 2a & 0 \\ 0 & \minus 2a & \minus 4a & 0 \end{matrix} } \\ \\ &\qquad\qquad\text{↓ 第 $1$ 列に沿って余因子展開} \\ \\ &= \minus \abs{ \begin{matrix} a^2 + 2a+1 & 2a^2 + 4a+2 & 5a^2 + 6a + 3 \\ 0 & \minus 2a & 0 \\ \minus 2a & \minus 4a & 0 \end{matrix} } \\ \\ &\qquad\qquad\text{↓ 第 $2$ 行に沿って余因子展開} \\ \\ &= \minus (\minus 2a) \cdot \abs{ \begin{matrix} a^2 + 2a+1 & 5a^2 + 6a + 3 \\ \minus 2a & 0 \end{matrix} } \\ \\ &= 2a (0 \minus (\minus 2a(5a^2 + 6a + 3))) \\ \\ &= 4a^2(5a^2 + 6a + 3) \end{align}
次の行列の行列式を計算せよ($i$ は虚数単位)。 $$ A = \pbr{ \begin{matrix} 2 + i & i & 1 \minus i \\ i & 2i & 1 \\ 1 & 1 + i & 2 \minus i \end{matrix} } $$
\begin{align} \det A &= \abs{ \begin{matrix} 2 + i & i & 1 \minus i \\ i & 2i & 1 \\ 1 & 1 + i & 2 \minus i \end{matrix} } \\ &&&\text{↓ 第 $3$ 列の $(\minus i)$ 倍を第 $1$ 列に加算} \\ &= \abs{ \begin{matrix} 1 & i & 1 \minus i \\ 0 & 2i & 1 \\ \minus 2i & 1 + i & 2 \minus i \end{matrix} } \\ &&&\text{↓ 第 $3$ 列の $(\minus 2i)$ 倍を第 $2$ 列に加算} \\ &= \abs{ \begin{matrix} 1 & \minus 2 \minus i & 1 \minus i \\ 0 & 0 & 1 \\ \minus 2i & \minus 1 \minus 3 i & 2 \minus i \end{matrix} } \\ &&&\text{↓ 第 $3$ 行に沿って余因子展開} \\ &= \minus \abs{ \begin{matrix} 1 & \minus 2 \minus i \\ \minus 2i & \minus 1 \minus 3 i \end{matrix} } \\ \\ &= \minus ((\minus 1 \minus 3 i) \minus (4i \minus 2)) \\ \\ &= \minus 1 + 7i \end{align}
次の行列の行列式を計算せよ($i$ は虚数単位)。 $$ A = \pbr{ \begin{matrix} 0 & i & 0 & 1 \\ i & 0 & \minus 1 & 0 \\ 0 & \minus 1 & 0 & \minus i \\ 1 & 0 & \minus i & 0 \end{matrix} } $$
\begin{align} \det A &= \abs{ \begin{matrix} 0 & i & 0 & 1 \\ i & 0 & \minus 1 & 0 \\ 0 & \minus 1 & 0 & \minus i \\ 1 & 0 & \minus i & 0 \end{matrix} } \\ &&&\text{↓ 第 $2$ 行の $i$ 倍を第 $4$ 行に加算} \\ &= \abs{ \begin{matrix} 0 & i & 0 & 1 \\ i & 0 & \minus 1 & 0 \\ 0 & \minus 1 & 0 & \minus i \\ 0 & 0 & \minus 2i & 0 \end{matrix} } \\ &&&\text{↓ 第 $4$ 行に沿って余因子展開} \\ &= \minus (\minus 2i) \abs{ \begin{matrix} 0 & i & 1 \\ i & 0 & 0 \\ 0 & \minus 1 & \minus i \end{matrix} } \\ &&&\text{↓ 第 $2$ 行に沿って余因子展開} \\ &= 2i \cdot (\minus 1) \cdot i \abs{ \begin{matrix} i & 1 \\ \minus 1 & \minus i \end{matrix} } \\ \\ &= 2 \cdot (1 \minus (\minus 1)) \\ \\ &= 4 \end{align}
\begin{align} \det A &= \abs{ \begin{matrix} 0 & i & 0 & 1 \\ i & 0 & \minus 1 & 0 \\ 0 & \minus 1 & 0 & \minus i \\ 1 & 0 & \minus i & 0 \end{matrix} } \\ &&&\text{↓ 第 $2$ 行の $i$ 倍を第 $4$ 行に加算} \\ &= \abs{ \begin{matrix} 0 & i & 0 & 1 \\ i & 0 & \minus 1 & 0 \\ 0 & \minus 1 & 0 & \minus i \\ 0 & 0 & \minus 2i & 0 \end{matrix} } \\ &&&\text{↓ 第 $1$ 行の $\minus i$ 倍を第 $3$ 行に加算} \\ &= \abs{ \begin{matrix} 0 & i & 0 & 1 \\ i & 0 & \minus 1 & 0 \\ 0 & 0 & 0 & \minus 2i \\ 0 & 0 & \minus 2i & 0 \end{matrix} } \\ &&&\text{↓ 左上と右下の行列に分解} \\ &= \abs{ \begin{matrix} 0 & i \\ i & 0 \end{matrix} } \abs{ \begin{matrix} 0 & \minus 2i \\ \minus 2i & 0 \end{matrix} } \\ \\ &= (0 \minus (\minus 1))(0 \minus (\minus 4)) \\ \\ &= 4 \end{align}