ヴィタリ集合|ルベーグ測度でも測れない集合
選択公理を使ってルベーグ非可測集合の存在を示す。
- $\NN$ は $0$ 以上の整数全体の集合とする。
- $\mu$ は $\RR$ 上のルベーグ測度とする。
- $A \subseteq \RR$ と $x \in \RR$ に対し $A + x = \iset{a + x}{a \in A}$ とする。
- 集合族 $\cbr{A_\lambda}_{\lambda \in \Lambda}$ が互いに素であるとは、$\lambda \neq \eta$ なる任意の $\lambda, \eta \in \Lambda$ に対し $A_{\lambda} \cap A_{\eta} = \varnothing$ であることをいう。
ルベーグ非可測集合が存在することの証明
選択公理を仮定したとき、ルベーグ可測でない集合 $A \subseteq \RR$ が存在する。
「$A$ はルベーグ非可測だ」と言えるのか考えてみよう
〇〇 を探そうってこと?
どんなことが成り立つのかというと……
$\mu$-可測な集合 $A \subseteq \RR$ に対し実数列 $\cbr{ x_n }_{n \in \NN}$ が条件
集合列 $\cbr{A + x_n}_{n \in \NN}$ は互いに素である
を満たすならば $$\displaystyle\mu\pbr{\bigcup_{n \in \NN} (A + x_n)} \in \cbr{0, \infty}$$ である。
可算加法性と平行移動不変性より \begin{align*} \mu \pbr{\bigcup_{n \in \NN} (A + x_n)} &= \sum_{n \in \NN} \mu(A + x_n) \\&= \sum_{n \in \NN} \mu(A) \\&= \begin{cases} 0 & (\mu(A) = 0) \\ \infty & (\mu(A) > 0) \end{cases} \end{align*}
交わらないように可算無限個平行移動させたら
それらの和集合の測度は $0$ か $\infty$ になる
$0$ にも $\infty$ にもなるはずがない
っていう集合はルベーグ非可測
集合 $A \subseteq \RR$ と実数列 $\cbr{ x_n }_{n \in \NN}$ が条件
- 集合列 $\cbr{A + x_n}_{n \in \NN}$ は互いに素である
- $0 \lt \mu(B) \leq \mu(C) \lt \infty$ なる $\mu$-可測集合 $B, C$ で $$B \subseteq \bigcup_{n \in \NN} (A + x_n) \subseteq C$$ となるものが存在する
をどちらも満たすとき、$A$ は $\mu$-可測ではない。
$A$ が $\mu$-可測であると仮定すると、補題1と条件 1. より $$\mu\pbr{\bigcup_{n \in \NN} (A + x_n)} \in \cbr{0, \infty}$$ であるが、一方条件 2. より $$0 \lt \mu\pbr{\bigcup_{n \in \NN} (A + x_n)} \lt \infty$$ であるので、矛盾する。
見つけたらゴールだね
区間を埋め尽くすことを考えると
互いに素にしなきゃいけない……
$A$ を作れば何とかなるかな?
選択公理を仮定したとき、ルベーグ可測でない集合 $A \subseteq \RR$ が存在する。
各 $\lambda \in \RR/\QQ$ に対し $\lambda \cap [0,1] \neq \varnothing$ であるので、選択公理より
任意の $\lambda \in \RR/\QQ$ に対し $a_\lambda \in \lambda \cap [0,1]$
となる実数の族 $\cbr{a_\lambda}_{\lambda\in\RR/\QQ}$ が存在する。
$A = \iset{a_\lambda}{\lambda \in \RR/\QQ}$ とする。
相異なる2つの有理数 $q, r$ に対し $A + q$ と $A + r$ は互いに素である。
もし $A + q$ と $A + r$ が共通の要素を持つと、 $$a_{\lambda} + q = a_{\eta} + r$$ となる $\lambda, \eta \in \RR / \QQ$ が存在する。 $a_{\lambda} + q \in \lambda$ と $a_{\eta} + r \in \eta$ から $\lambda \cap \eta \neq \varnothing$ がわかる。共通の要素を持つ同値類は一致するので $\lambda = \eta$ となり、したがって $q = r$ を得る。
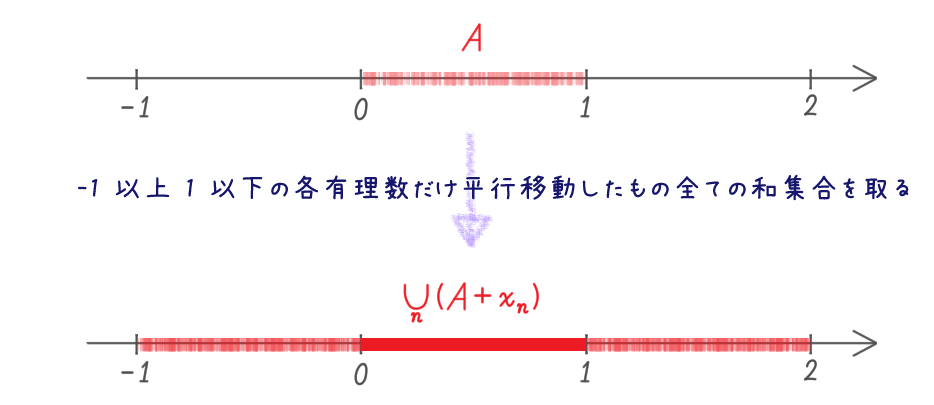
$\displaystyle[0,1] \subseteq \bigcup_{q \in \QQ \cap [-1,1]} (A + q)\subseteq [-1, 2]$ が成り立つ。
$x \in [0,1]$ を任意に取ると、 $a_{x + \QQ} \in x + \QQ$ なので $a_{x + \QQ} + q = x$ となる $q \in \QQ$ が存在し、 従って $x \in A + q$ を得る。
また $q = x \minus a_{x + \QQ}$ であるが $x, a_{x + \QQ} \in [0,1]$ より $q \in [-1,1]$ である。
$A \subseteq [0, 1]$ なので各 $q \in \QQ \cap [-1,1]$ に対し $A + q \subseteq [-1,2]$ である。
実数列 $\cbr{x_n}_{n \in \NN}$ を $$\iset{x_n}{n \in \NN} = \QQ \cap [-1,1]$$ となるように取る。ただし $n \neq m$ ならば $x_n \neq x_m$ とする。
主張1より
$\cbr{A + x_n}_{n \in \NN}$ は互いに素
であり、主張2より $$[0,1] \subseteq \bigcup_{n \in \NN}\pbr{A + x_n} \subseteq [-1,2]$$ であるので、補題2より $A$ は $\mu$-可測ではない。
ヴィタリ集合とルベーグ積分できない関数
リーマン積分可能
リーマン積分不可能だけどルベーグ積分可能
ルベーグ非可測な集合の存在が分かって……
$[0,1]$ 区間でルベーグ積分不可能
ルベーグ積分できない例」としてよく
ルベーグ積分できない例」としては
面白いんだけど
として挙げるには
ヴィタリ集合の指示関数の方がグサッとくる
非可算無限個の非空集合たちから
1つずつ選んだけど)
どんな集合もルベーグ可測になるような公理系に
なったりしないかな……?)