集合を使って「写像」を作る|順序対・直積・写像の構成
集合を使って「写像」を構成する。
数学は集合からできてる?
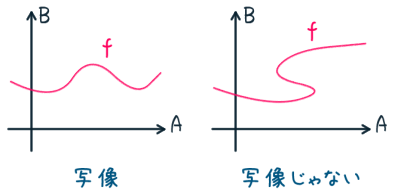
写像とは?
「集合 $A$ の各元に対して集合 $B$ の元を対応させる規則」
とかって教えられたけど
自然数とは?
ペアノの公理を満たす集合の要素?
ってことを一度やっとくと
だいぶすっきりすると思います
順序対を集合から構成する方法
集合の「直積」を定義したい
集合 $a, b$ に対し、集合 $(a, b)$ を $$(a, b) = \cbr{\cbr{a}, \cbr{a, b}}$$ で定める。この形の集合を順序対と呼ぶ。
$(a, b) = (c, d)$ ならば $a = c$ かつ $b = d$
っていう順序対が持つべき性質を導ける
集合 $a, b, c$ に対し $\cbr{a, b} = \cbr{a, c}$ ならば $b = c$ である。
$b \in \cbr{a, b} = \cbr{a, c}$ より
であり、また $c \in \cbr{a, c} = \cbr{a, b}$ より
なので、「$b = a$ かつ $c = a$」のときもそうでないときも $b = c$ を得る。
集合 $a, b, c, d$ に対し、$(a, b) = (c, d)$ ならば
が成り立つ。
$\cbr{a} \in \cbr{\cbr{a}, \cbr{a, b}} = \cbr{\cbr{c}, \cbr{c, d}}$ なので
であり、いずれの場合も $c \in \cbr{a}$ すなわち $a = c$ を得る。従って $$\cbr{\cbr{a}, \cbr{a, b}} = \cbr{\cbr{a}, \cbr{a, d}}$$ であり、補題を2度用いて $b = d$ を得る。
$a = b$ かつ $b = a$ ってなるから……
集合 $a, b$ に対し $a \neq b$ ならば $(a, b) \neq (b, a)$ である。
$(a, (b, c))$ で定義すればいいのかな
$f: \cbr{0,1,2} \rightarrow \cbr{a,b,c}$
$f(0) = a, f(1) = b, f(2) = c$
っていう写像を $(a, b, c)$ とする
っていう手も
直積(デカルト積)を構成する方法
直積も定義できる
集合 $A, B$ に対し、集合 $A \times B$ を $$A \times B = \iset{(a, b)}{\text{$a \in A$ and $b \in B$}}$$ で定め、$A$ と $B$ の直積と呼ぶ。
分出公理をつかってチェックすべきだけど…)
写像を集合から構成する方法
集合 $B$ の要素がただ一つ定まるような集合を
写像ということにしよう
集合 $A, B$ の直積 $A \times B$ の部分集合 $f$ が、各 $a \in A$ に対して条件
を満たすとき、$f$ を $A$ から $B$ への写像と呼び $f: A \rightarrow B$ と書く。 また、この $b$ を $f(a)$ と書く。
写像 $f: A \rightarrow B$ において $A$ を始域(あるいは定義域)、$B$ を終域と呼ぶ。
写像というものを作ったわけか
写像 $f: A \rightarrow B$ と $A$ の部分集合 $A’$ に対し $$f[A’] = \iset{f(a)}{a \in A’}$$ とし、$A’$ の $f$ による像と呼ぶ。
$A’$ の像まで $f(A’)$ って書いちゃうと
それが像なのか写像の行先なのかが分かりにくいから……
写像 $f: A \rightarrow B$ が各 $a_1, a_2 \in A$ に対し、
を満たすとき、$f$ は単射であるという。一方、 $$f[A] = B$$ を満たすとき、$f$ は全射であるという。
写像が単射でも全射でもあるとき、その写像は全単射であるという。
(おまけ)そもそも集合って?
って感じできっちり公理化されてる
「$\iset{x}{x \not\in x}$ を集合と認めると
矛盾が生じる! やべぇ!」
って問題になったことがあったんだけど
$\iset{x}{x \not\in x}$ を「集合」の枠組みから
排除できるようになったりしたりね
あまり深入りしないでおこう
一回素朴に集合から写像や自然数を作る様子を眺めて
感覚をつかんでからでもいいと思う
「ZFC 公理系」とか「公理的集合論」とかで
ググるべし

 https://sorai-note.com/math/200403/
https://sorai-note.com/math/200403/