半順序・全順序・狭義半順序・狭義全順序
半順序・全順序・狭義半順序・狭義全順序とそれらの関係について学ぶ。
- $\NN$ を非負整数全体の集合とする。
- $\NN_+$ を正整数全体の集合とする。
- 集合 $X$ のべき集合を $\mathcal{P}(X)$ と書く。
二項関係とは
集合 $X$ に対し、直積 $X \times X$ の部分集合を $X$ 上の二項関係と呼ぶ。
集合 $\iset{(x,y)}{x, y \in X}$ のこと
直積の定義 ↓
集合 $X$ 上の二項関係 $R$ と $x, y \in X$ に対し、$(x,y) \in R$ であることを $$x \mathrel{R} y$$ と表す。
${\rightarrow} = \cbr{(0,1), (1,0), (1,2)}$ は $\cbr{0,1,2}$ 上の二項関係であり、 \begin{align*} &0 \rightarrow 1 && 1 \rightarrow 0 && 1 \rightarrow 2 \end{align*} であるが、$2 \rightarrow 0$ ではない。
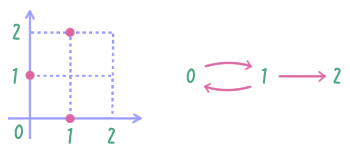
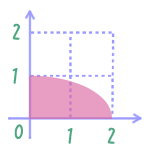
$\iset{(x,y) \in [0,2]^2}{ x^2 + 4y^2 \leq 4 }$ は $[0,2]$ 上の二項関係である。
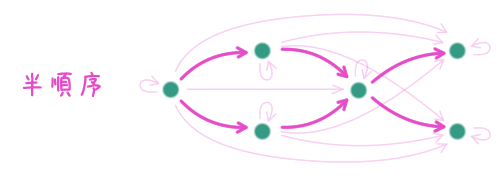
半順序と全順序
集合 $X$ 上の二項関係 $\leq$ が半順序(partial order)であるとは
(reflexivity)
各 $x \in X$ に対し $$x \leq x$$
(antisymmetricity)
各 $x,y \in X$ に対し
$(x \leq y$ かつ $y \leq x)$ ならば $x = y$
(transitivity)
各 $x,y,z \in X$ に対し
$(x \leq y$ かつ $y \leq z)$ ならば $x \leq z$
を満たすこと。更に
(connexity)
各 $x,y \in X$ に対し
$x \leq y$ または $y \leq x$
も成り立つ半順序を全順序(total order)あるいは線形順序(linear order)と呼ぶ。
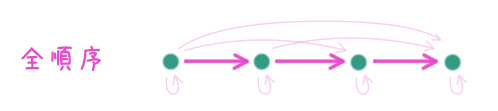
$\NN$ 上の通常の順序 $\leq$ は $\NN$ 上の二項関係として全順序である。
集合 $X$ が異なる2要素 $a, b \in X$ を持つとき、集合 $X$ 上の二項関係$$R = X \times X$$は半順序ではない。
$a \mathrel{R} b$ と $b \mathrel{R} a$ が成り立つ一方で $$a \neq b$$ であるので、$R$ は反対称律を満たさない。したがって $R$ は半順序ではない。
集合 $X$ が異なる2要素 $a, b \in X$ を持つとき、$\mathcal{P}(X)$ 上の包含関係 $${\subseteq} = \iset{(A, B) \in \mathcal{P}(X)^2 }{ \forall a \in A, a \in B}$$ は半順序であるが全順序ではない。
半順序であることは自明。全順序でないことは
$\cbr{a} \not\subseteq \cbr{b}$ かつ $\cbr{b} \not\subseteq \cbr{a}$
からわかる。
$\RR \setminus \cbr{0}$ 上の二項関係 $$R = \iset{(x, y) \in (\RR \setminus \cbr{0})^2}{\frac{y}{x} \in \NN_+} $$ は半順序であるが全順序でない。
$\displaystyle\frac{x}{x} = 1 \in \NN_+$ である。
$\displaystyle\frac{y}{x} = k$ も $\displaystyle\frac{x}{y} = m$ も正整数であるとすると、$km = 1$ なので $$k = m = 1$$ となり、したがって $x = y$ である。
$\displaystyle\frac{y}{x}$ も $\displaystyle\frac{z}{y}$ も正整数ならば、それらの積 $$\frac{y}{x} \cdot \frac{z}{y}= \frac{z}{x}$$ も正整数である。
$\displaystyle\frac{2}{3}$ も $\displaystyle\frac{3}{2}$ も正整数でない。
半順序・全順序を逆向きにする
全順序を逆向きにしても全順序
集合 $X$ 上の半順序 $\leq$ に対し、二項順序 $\geq$ を $${\geq} = \iset{(x,y) \in X^2}{y \leq x}$$ で定めると、$\geq$ も半順序。
また、$\leq$ が全順序なら $\geq$ も全順序。
反射律、反対称律は自明。$x \geq y$ かつ $y \geq z$ のときは
$z \leq y$ かつ $y \leq x$
となり、$\leq$ の推移律より $z \leq x$ すなわち $x \geq z$ なので、$\geq$ の推移律を得る。
$\leq$ が全順序律を持つとき $\geq$ も全順序律を持つことは自明。
狭義半順序と狭義全順序
集合 $X$ 上の二項関係 $\lt$ が狭義半順序(strict partial order)であるとは
(irreflexivity)
各 $x \in X$ に対し $$x \mathrel{\not\lt} x$$
(transitivity)
各 $x,y,z \in X$ に対し
$(x \lt y$ かつ $y \lt z)$ ならば $x \lt z$
を満たすこと。更に
(trichotomy)
各 $x,y \in X$ に対し \begin{align*} &x \mathrel{\lt} y && y \mathrel{\lt} x && x = y \end{align*} のいずれか一つだけが成立する
も成り立つ狭義半順序を狭義全順序(strict total order)と呼ぶ。
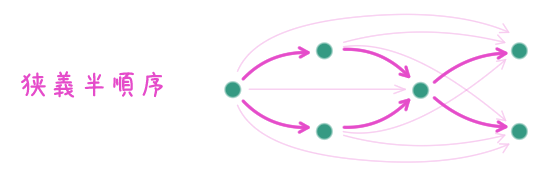

集合 $X$ 上の狭義半順序 $\lt$ に対し
(asymmetricity)
各 $x, y \in X$ に対し
$x \mathrel{\lt} y$ ならば $y \mathrel{\not\lt} x$
が成り立つ。
もし $x \lt y$ かつ $y \lt x$ ならば推移律より $x \lt x$ となり非反射律に反する。
$\NN$ 上の通常の順序 $\lt$ は $\NN$ 上の二項関係として狭義全順序である。
狭義半順序・狭義全順序を逆向きにする
狭義全順序を逆向きにしても狭義全順序
集合 $X$ 上の狭義半順序 $\lt$ に対し、二項順序 $\gt$ を $${\gt} = \iset{(x,y) \in X^2}{y \lt x}$$ で定めると、$\gt$ も狭義半順序。
また、$\lt$ が狭義全順序なら $\gt$ も狭義全順序。
非反射律は自明。推移律は半順序のときの証明と同じ。
$\lt$ が三分律を持つとき $\gt$ も三分律を持つことは自明。
半順序から狭義半順序を作る
集合 $X$ 上の半順序 $\leq$ が与えられたとき、$X$ 上の二項関係 $\lt$ を $$ {\lt} = \iset{(x,y) \in X^2}{x \leq y \mathrel{\text{and}} x \neq y} $$ で定めると、$\lt$ は $X$ 上の狭義半順序になる。
更に $\leq$ が全順序でもあれば、この $\lt$ は狭義全順序になる。
また逆に $\leq$ が全順序でないならば、この $\lt$ は狭義全順序ではない。
任意の $x \in X$ に対し $x \not\lt x$ であることは $\lt$ の定義より自明。
$x \lt y$ かつ $y \lt z$ であるとする。$\leq$ の推移性より $$x \leq z$$ である。ここで仮に $x = z$ であるとすると、$\leq$ の反対称律と $x \leq y$ と $y \leq x$ から $x = y$ となり、$x \lt y$ に反するので、 $$x \neq z$$ である。以上により $x \lt z$ を得る。
$\leq$ は全順序であるとする。
$x \lt y$ と $y \lt x$ が両立しないことは非反射律と推移律からわかる。
$x \lt y$ と $x = y$ が両立しないことは非反射律からわかる。
$y \lt x$ と $x = y$ が両立しないことも非反射律からわかる。
三分律の三条件のいずれかが成り立つことを示すために、
$x \not\lt y$ かつ $y \not\lt x$
を仮定して $x = y$ を示す。$x \not\lt y$ より
$x \not\leq y$ または $x = y$
であり、更に $y \not\lt x$ より
$y \not\leq x$ または $x = y$
であるが、$\leq$ の全順序律より $x \not\leq y$ か $y \not\leq x$ の少なくともどちらかは偽である。したがって $x = y$ である。
$\leq$ は全順序でないとする。
$\leq$ は全順序でないので、 $x \not\leq y$ かつ $y \not\leq x$ となる $x, y \in X$ が存在する。このとき
$x \not\lt y$ かつ $y \not\lt x$
である。一方 $\leq$ の反射律と $x \not\leq y$ から、$$x \neq y$$ である。 以上により、$x \lt y$ も $y \lt x$ も $x = y$ も成り立たない $x, y \in X$ の存在を得て、三分律が成り立たないことがわかった。
狭義半順序から半順序を作る
集合 $X$ 上の狭義半順序 $\lt$ が与えられたとき、$X$ 上の二項関係 $\leq$ を $$ {\leq} = \iset{(x,y) \in X^2}{x \lt y \mathrel{\text{or}} x = y} $$ で定めると、$\leq$ は $X$ 上の半順序になる。
更に $\lt$ が狭義全順序でもあれば、この $\leq$ は全順序になる。
また逆に $\lt$ が狭義全順序でないならば、この $\leq$ は全順序ではない。
任意の $x \in X$ に対し $x \leq x$ となることは $\leq$ の定義より自明。
$x \leq y$ かつ $y \leq x$ であるとすると、
$x \lt y$ または $x = y$
および
$y \lt x$ または $x = y$
が成り立つ。しかし $x \lt y$ と $y \lt x$ が両立しないことは $\lt$ の推移律と非反射律からわかる。したがって $x = y$ を得る。
$x \leq y$ かつ $y \leq z$ であるとすると、
$x \lt y$ または $x = y$
および
$y \lt z$ または $y = z$
が成り立つが、
- $x \lt y$ かつ $y \lt z$ ならば、 $\lt$ の推移律より $x \lt z$
- $x \lt y$ かつ $y = z$ ならば、 $x \lt z$
- $x = y$ かつ $y \lt z$ ならば、 $x \lt z$
- $x = y$ かつ $y = z$ ならば、 $x = z$
でいずれの場合も $x \leq z$ である。
$\lt$ は狭義全順序であるとする。
$x, y \in X$ を任意に取る。$x \not\leq y$ を仮定して $y \leq x$ を示す。$x \not\leq y$ から
$x \not\lt y$ かつ $x \neq y$
であるので、$\lt$ の三分律により $y \lt x$ であり、特に $y \leq x$ である。
$\lt$ は狭義全順序でないとする。
$\lt$ が狭義全順序でないので、
$x \not\lt y$ かつ $y \not\lt x$ かつ $x \neq y$
となる $x, y \in X$ が存在する。$x \not\lt y$ と $x \neq y$ より $$x \not\leq y$$ であり、一方 $y \not\lt x$ と $x \neq y$ より $$y \not\leq x$$ である。つまり $x \leq y$ も $y \leq x$ も成り立たない $x, y \in X$ が存在し、$\leq$ が全順序律を満たさないことがわかる。