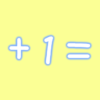自然数上に通常の全順序・狭義全順序を構成する
自然数上に通常の全順序・狭義全順序を（加法を使って）構成する。
自然数上の加法
自然数上の加法を構成しました
https://sorai-note.com/math/200404/写像 $+: \NN \times \NN \rightarrow \NN$ で
を満たすものが唯一つ存在する。
$(\NN, +)$ は可換モノイドである。
自然数上の通常の順序を作るよ
- 自然数 $n, m$ に対し $s(n + m) = n + s(m) = s(n) + m$ である。
- 自然数 $n, m$ が $n + m = 0$ を満たすならば $n = m = 0$ である。
- 自然数 $n, m$ に対し、$n + k = m$ となる自然数 $k$ は存在すれば唯一つ。
- 自然数 $n, k$ に対し、$n + k = n$ ならば $k = 0$ である。
自然数上に全順序を構成する
前にやったね
次のように定めます
$\NN$ 上の二項関係 $\leq$ を $${\leq} = \iset{(n, m) \in \NN^2}{\exists k \in \NN, n + k = m}$$ で定める。
自然数 $n$ に対し $n \leq s(n)$ が成り立つ。
$n + s(0) = s(n + 0) = s(n)$ より従う。
自然数 $n, m$ に対し、
（$n \leq m$ かつ $n \neq m$） $\quad$ ならば $\quad$ $s(n) \leq m$
が成り立つ。$n \leq m$ より $n + k = m$ となる自然数 $k$ が存在するが、$n \neq m$ なので $k \neq 0$ であり、$k = s(\ell) \ (\ell \in \NN)$ と書ける。このとき $n + s(\ell) = m$ なので $$s(n) + \ell = n + s(\ell) = m$$ となり、$s(n) \leq m$ を得る。
$\leq$ は $\NN$ 上の全順序である。
$n + 0 = n$ なので $n \leq n$ である。
$n \leq m$ かつ $m \leq n$ のとき、ある自然数 $k_1, k_2$ により
$n + k_1 = m$$\quad$ かつ $\quad$$m + k_2 = n$
となる。このとき $$n + k_1 + k_2 = m + k_2 = n$$ なので $k_1 + k_2 = 0$ となり、$k_1 = k_2 = 0$ を得る。したがって $n = m$ である。
$n \leq m$ かつ $m \leq \ell$ のとき、ある自然数 $k_1, k_2$ により
$n + k_1 = m$$\quad$ かつ $\quad$$m + k_2 = \ell$
となる。このとき $$n + k_1 + k_2 = m + k_2 = \ell$$ なので $n \leq \ell$ である。
「$n \leq m$ または $m \leq n$」を $n$ についての数学的帰納法で示す。
$0 + m = m$ なので $0 \leq m$ である。
$\NN$ 上の二項関係 $\geq$ を $${\geq} = \iset{(n,m) \in \NN^2}{m \leq n}$$ で定める。
$\geq$ は $\NN$ 上の全順序である。
自然数上に狭義全順序を構成する
前にやったね
次のように定めます
$\NN$ 上の二項関係 $\lt$ を $${\lt} = \iset{(n, m) \in \NN^2}{n \leq m \mathrel{\text{かつ}} n \neq m}$$ で定める。
$\lt$ は $\NN$ 上の狭義全順序である。
$\NN$ 上の二項関係 $\gt$ を $${\gt} = \iset{(n,m) \in \NN^2}{m \lt n}$$ で定める。
$\gt$ は $\NN$ 上の狭義全順序である。
（補足）集合論から見てみると……
各 $n, m \in \NN$ に対し $n \lt m$ と $n \in m$ は同値。
$m$ についての帰納法で示す。
$n \lt 0$ も $n \in \varnothing$ も偽である。
$n \lt s(m)$ と補題２より $s(n) \leq s(m)$ であり、$s(n) + k = s(m)$ なる $k \in \NN$ が存在して $$s(n + k) = s(m)$$ と $s$ の単射性より $n + k = m$ すなわち $n \leq m$ である。
$n = m$ のときは $n = m \in s(m)$ である。
$n \lt m$ のときは帰納法の仮定より $n \in m$ であり、$m \subseteq s(m)$ から $n \in s(m)$ を得る。
$n \in m \cup \cbr{m}$ より「$n \in m$ または $n = m$」であり、帰納法の仮定より
$n \lt m$ または $n = m$
すなわち $n \leq m$ である。よって $m \lt s(m)$ を用いて $n \lt s(m)$ を得る。