始域や終域が空集合の写像｜空関数と単射性と全射性

2020/05/182020/06/26

始域や終域が空集合の写像って？

始域とか終域が空集合の写像ってあるの？
$f: \varnothing \rightarrow \NN$ とか
$g: \NN \rightarrow \varnothing $ とか
$h: \varnothing \rightarrow \varnothing $ とか

写像の定義にもどるべし

集合を使って「写像」を作る｜順序対・直積・写像の構成

今日の目標集合を使って「写像」を構成する。数学は集合からできてる？質問１写像とは？授業では ...

https://sorai-note.com/math/200402/

定義

集合 $A, B$ の直積 $A \times B$ の部分集合 $f$ が、各 $a \in A$ に対して条件

$(a, b) \in f$ なる $b \in B$ がただ一つ存在する

を満たすとき、$f$ を $A$ から $B$ への写像と呼び $f: A \rightarrow B$ と書く。

まず $B \neq \varnothing$ として
写像 $f: \varnothing \rightarrow B$ について考えよう

$\varnothing \times B$ とは何？

$A \times B$ の定義は $\iset{(a,b)}{a \in A, b \in B}$ だから……

$\varnothing \times B = \iset{(a,b)}{a \in \varnothing, b \in B}$ となって
$a \in \varnothing$ は常に偽だから……

$\varnothing \times B = \varnothing$

じゃあ $\varnothing \times B$ の部分集合は

$\varnothing$ だけだね

じゃあ $f = \varnothing$ としたときに
$f: \varnothing \rightarrow B$ は写像？

$f$ が写像とは $$\forall a \in A, \exists! b \in B, (a,b) \in f$$ だから今の場合だと $$\forall a \in \varnothing, \exists! b \in B, (a,b) \in \varnothing$$

$\forall a \in \varnothing$ ってどう読めばいいんだっけ

$「\forall a \in A, P(a)」$ は
論理式 $\forall a (a \in A \Rightarrow P(a))$ の略記だから……

$「\forall a \in \varnothing, P(a)」$ は
$\forall a (a \in \varnothing \Rightarrow P(a))$ の略記か

これは真だね

したがって $\varnothing$ は $\varnothing$ から $B$ への写像

$\varnothing$ 以外に写像の候補は無いから
$\varnothing$ から $B$ への写像は $\varnothing$ だけってことか

他の場合もまとめるとこんな感じ

記法

集合 $X, Y$ に対し $X$ から $Y$ への写像全体を $\mathcal{F}(X, Y)$ と書くことにする。

命題

空でない集合 $A, B$ に対し \begin{align} \mathcal{F}(\varnothing, B) &= \cbr{\varnothing} \\ \mathcal{F}(A, \varnothing) &= \varnothing \\ \mathcal{F}(\varnothing, \varnothing) &= \cbr{\varnothing} \end{align} である。

証明

$\mathcal{F}(\varnothing, B) = \cbr{\varnothing}$ であること

$\varnothing \times B = \varnothing$ であり、その部分集合は $\varnothing$ だけである。また $$\forall a \in \varnothing, \exists! b \in B, (a,b) \in \varnothing$$ は真なので、$\varnothing$ は $\varnothing$ から $B$ への写像である。

$\mathcal{F}(A, \varnothing) = \varnothing$ であること

$A \times \varnothing = \varnothing$ であり、その部分集合は $\varnothing$ だけである。また $A \neq \varnothing$ なので $$\forall a \in A, \exists! b \in \varnothing, (a,b) \in \varnothing$$ は偽である。よって $\varnothing$ から $B$ への写像は存在しない。

$\mathcal{F}(\varnothing, \varnothing) = \cbr{\varnothing}$ であること

$\varnothing \times \varnothing = \varnothing$ であり、その部分集合は $\varnothing$ だけである。また $$\forall a \in \varnothing, \exists! b \in \varnothing, (a,b) \in \varnothing$$ は真なので、$\varnothing$ は $\varnothing$ から $\varnothing$ への写像である。

$f: \varnothing \rightarrow \NN$ は唯一つ存在して $f = \varnothing$
$g: \NN \rightarrow \varnothing $ は存在しない
$h: \varnothing \rightarrow \varnothing $ は唯一つ存在して $h = \varnothing$
ってことか

ちなみに始域が $\varnothing$ の写像は
空関数って呼ばれたりするよ

空関数は単射？全射？

じゃあ次はその空関数が
単射かどうか全射かどうか
が気になるよね

えっ？あうん…… そだね……

写像 $f: A \rightarrow B$ が単射とは $$\forall a_1, a_2 \in A, (f(a_1) = f(a_2) \implies a_1 = a_2)$$ ってことだけど……

$f = \varnothing$ のときに $\varnothing(a_1)$ って書くのに抵抗あるなら \begin{align} \forall a_1, a_2 &\in A, \forall b \in B, \\&((a_1, b) \in f \land (a_2, b) \in f \implies a_1 = a_2) \end{align} に戻して考えたらいいね

$A = \varnothing$ のときこれは真だね

一方
写像 $f: A \rightarrow B$ が全射とは \begin{align} \forall b \in B, \exists a \in A, (a, b) \in f \end{align}

これは
$A = \varnothing, B \neq \varnothing$ のときは偽で
$A = B = \varnothing$ のときは真か

命題

集合 $B$ は空でないとする。このとき

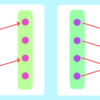
$\varnothing: \varnothing \rightarrow B$ は単射であるが全射でない。

$\varnothing: \varnothing \rightarrow \varnothing$ は全単射である。

証明

$\varnothing: \varnothing \rightarrow B$ が単射であること
$\varnothing: \varnothing \rightarrow \varnothing$ が単射であること

これらの主張は $\forall a_1, a_2 \in \varnothing, P(a_1, a_2)$ の形の命題なので真。

$\varnothing: \varnothing \rightarrow B$ が全射でないこと

$b \in B$ を一つ取ると $\exists a \in \varnothing, (a, b) \in \varnothing$ は偽なので全射ではない。