鳩ノ巣原理を証明する|有限集合の定義
有限集合を定義し、鳩の巣原理とその双対・逆・双対の逆を示す。
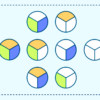
鳩の巣原理とは
全ての鳩を巣に入れたら
2羽以上鳩が入ってる巣が絶対ある
ってのだっけ
鳩の集合を $A$、巣の集合を $B$ として
$A$ の要素数が $B$ の要素数より真に大きいとき
$A$ から $B$ への対応 $f: A \rightarrow B$ をどのように与えても
$f(a_1) = f(a_2)$ となる2羽の鳩 $a_1 \neq a_2$ がいるって感じかな
有限集合 $A, B$ に対し、$\abs A \gt \abs B$ ならば $A$ から $B$ への単射は存在しない。
すぐ終わるんじゃないの?
有限集合とは
これから定義するね
自然数 $n \in \NN$ に対し、$[n]$${} = \iset{i \in \NN}{1 \leq i \leq n}$ と書く。
集合 $X$ が有限集合であるとは、
ある自然数 $n$ に対し、全単射 $f: [n] \rightarrow X$ が存在する
こととする。有限集合でない集合を無限集合と呼ぶ。$\cbr{2,3,5}$ は有限集合。実際 $f: [3] \rightarrow \cbr{2,3,5}$ を
$f(1) = 2 \qquad f(2) = 3 \qquad f(3) = 5$
で定義すると $f$ は全単射。恒等写像 $\text{id}_{[n]} : [n] \rightarrow [n], \ \text{id}_{[n]}(i) = i$ が
全単射だからね
空関数 $\varnothing : \varnothing \rightarrow \varnothing$ は全単射だから
$\varnothing$ から $B$ への写像は唯一つ存在して 単射だけど全射じゃない
$\varnothing$ から $\varnothing$ への写像は唯一つ存在して 全単射
$A$ から $\varnothing$ への写像は存在しない
いろいろ使うから
慣れてない人はこっちを
ざっと眺めとくといいかもです↓
「全射と全射の合成は全射」
「全単射が存在したら逆写像が存在して全単射」
「$X\neq\varnothing$ で単射 $X \rightarrow Y$ が存在したら
全射 $Y \rightarrow X$ が存在する」
とかを使うよ
有限集合の「要素数」とは
自然数 $n$ があるから
その $n$ を $\abs X$ として定義したらいいんじゃないの?
全単射 $f: [n] \rightarrow X$ も
全単射 $g: [m] \rightarrow X$ も
存在するようなことがあったら
それは定義として破綻してる
あり得ないことをちゃんと証明しなきゃね
全単射 $f: [n] \rightarrow X$ と全単射 $g: [m] \rightarrow X$ があると仮定すると
全単射 $g^{-1} \circ f: [n] \rightarrow [m]$ が作れて
そこから矛盾を導く とかかな?
$[n]$ から $[m]$ への単射があるときの $n$ と $m$ の関係を
チェックしてみようか
自然数 $n,m$ に対し、$[n]$ から $[m]$ への全射が存在するならば $n \geq m$ である。
各 $n \in \NN$ に対し、命題
各 $m \in \NN$ に対し「$[n]$ から $[m]$ への全射が存在するならば $n \geq m$」
を $n$ についての数学的帰納法で示す。$[n]$ から $[m]$ への全射が存在するとする。いま $[n] = [0] = \varnothing$ だが、空集合から空でない集合への写像は全射ではないので
$[m]$ は空集合
である。よって $m = 0$ であり、$n \geq m$ が成立。全射 $f: [n + 1] \rightarrow [m]$ が存在するとして $n + 1 \geq m$ を示す。$[n + 1] \neq \varnothing$ であるが、空でない集合から空集合への写像は存在しないので $m \geq 1$ であることに注意。
$f$ の $[n]$ への制限写像を $\tilde{f}$ とする。すなわち $$\tilde{f}: [n] \rightarrow [m], \qquad \tilde{f}(i) = f(i) \quad (i \in [n])$$ である。
$\tilde{f}$ の全射性を示す。 $\ell \in [m]$ を任意に取る。このとき $f$ の全射性より
$f(i) = \ell$ となる $i \in [n + 1]$ が存在
する。ここで- $i \lt n + 1$ のとき、$\tilde{f}(i) = f(i) = \ell$
- $i = n + 1$ のとき、$\tilde{f}(k) = f(k) = f(n + 1) = \ell$
となるので $\tilde{f}: [n] \rightarrow [m]$ は全射。よって帰納法の仮定より $n \geq m$ となり $n + 1 \geq m$ を得る。
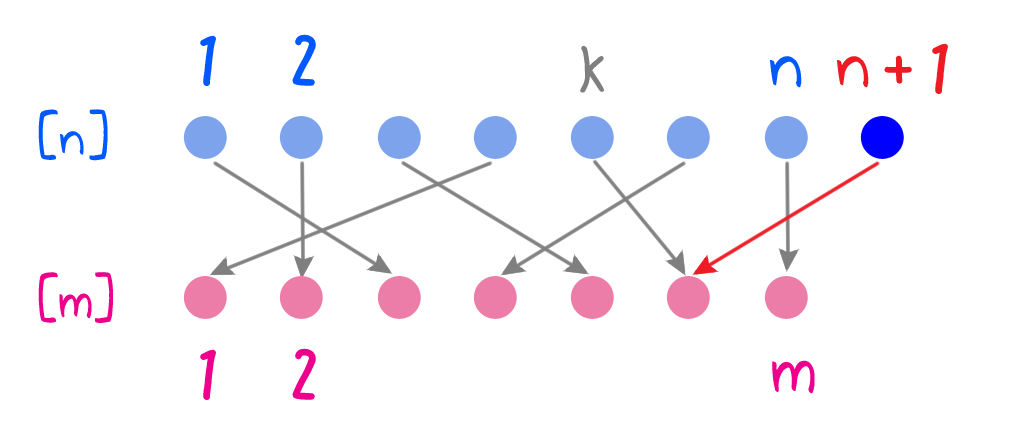
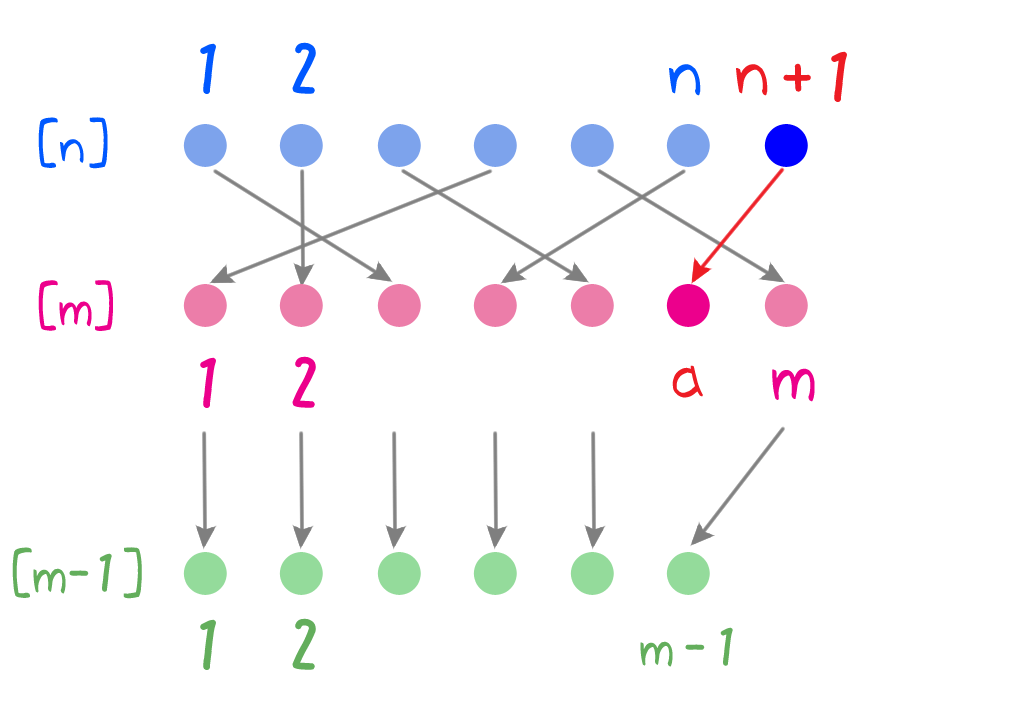
$a = f(n + 1)$ とする。$\tilde{f}(k) = a$ となる $k \in [n]$ は存在しないので、終域を制限した写像 $$\tilde{f}: [n] \rightarrow [m] \setminus \cbr{a}$$ を考えることができ、これが全射であることは $f$ の全射性から分かる。
写像 $g: [m] \setminus \cbr{a} \rightarrow [m-1]$ を $$g(i) = \begin{cases} i & (\text{$i \lt a$ のとき})\\ i – 1 & (\text{$i \gt a$ のとき}) \end{cases}$$ とすると $g$ は全射なので $g \circ \tilde{f}: [n] \rightarrow [m-1]$ も全射である。よって帰納法の仮定より $n \geq m – 1$ であり $n + 1 \geq m$ を得る。
ちゃんと証明書くと長いなあ……
自然数 $n,m$ に対し、$[n]$ から $[m]$ への単射が存在するならば $n \leq m$ である。
結論 $n \leq m$ が常に成立。
$[n] \neq \varnothing$ であること、そして $[n]$ から $[m]$ への単射が存在することから、$[m]$ から $[n]$ への全射も存在する。よって命題1より $m \geq n$ である。
有限集合 $X$ に対し、全単射 $f: [n] \rightarrow X$ が存在するような自然数 $n$ はただ一つである。
自然数 $n,m$ に対し、全単射 $f: [n] \rightarrow X$ と $g: [m] \rightarrow X$ が存在するとする。このとき $$g^{-1} \circ f: [n] \rightarrow [m]$$ も全単射。よって命題1と命題2より $n \geq m$ かつ $m \geq n$ となり、$n = m$ を得る。
有限集合 $X$ に対し、全単射 $f: [n] \rightarrow X$ が存在するような(唯一つの)自然数 $n$ を $X$ の要素数と呼び $\abs X$ と書く。
自然数 $n$ に対し $\abs{[n]} = n$ である。実際、恒等写像 $\text{id}_n: [n] \rightarrow [n]$ は全単射である。
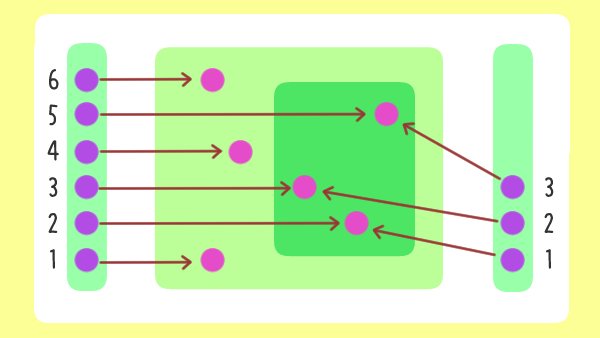
鳩の巣原理の証明
有限集合 $A, B$ に対し、
$\abs A \gt \abs B$ ${}\implies{}$ $A$ から $B$ への単射は存在しない
$n = \abs A$ および $m = \abs B$ とし、全単射 $g_A: [n] \rightarrow A$ と $g_B: [m] \rightarrow B$ を取る。もし単射 $f: A \rightarrow B$ が存在すれば、 $$g_B^{-1} \circ f \circ g_A: [n] \rightarrow [m]$$ も単射になり、命題2より $n \leq m$ となり矛盾。
鳩の巣原理の双対
有限集合 $A, B$ に対し、
$\abs A \lt \abs B$ ${}\implies{}$ $A$ から $B$ への全射は存在しない
$n = \abs A$ および $m = \abs B$ とし、全単射 $g_A: [n] \rightarrow A$ と $g_B: [m] \rightarrow B$ を取る。もし全射 $f: A \rightarrow B$ が存在すれば、 $$g_B^{-1} \circ f \circ g_A: [n] \rightarrow [m]$$ も全射になり、命題1より $n \geq m$ となり矛盾。
鳩の数より巣の数の方が多いなら
空の巣が絶対にあるってことか
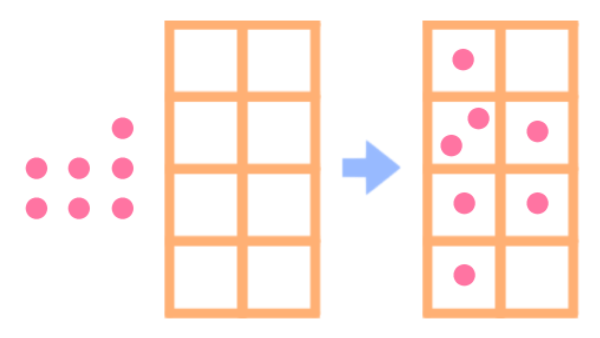
鳩の巣原理の逆
っていう命題
有限集合 $A, B$ に対し、
$A$ から $B$ への単射が存在しない ${}\implies{}$ $\abs A \gt \abs B$
$n = \abs A$ および $m = \abs B$ とする。対偶を示す。つまり $n \leq m$ を仮定し、$A$ から $B$ への単射を構成する。
全単射 $g_A: [n] \rightarrow A$ と $g_B: [m] \rightarrow B$ を取り、写像 $h: [n] \rightarrow [m]$ を $h(i) = i$ で定義すると $h$ は単射。よって $$g_B \circ h \circ g_A^{-1}: A \rightarrow B$$ も単射である。
次が言えるわけだね
有限集合 $A, B$ に対し、
$\abs A \leq \abs B$ $~\iff~$ $A$ から $B$ への単射が存在する
鳩の巣原理の双対の逆
「$A$ から $B$ への全射が存在しないなら $\abs A \lt \abs B$」
も言えるかな?
空でない集合から空集合への写像は
そもそも存在しないということ
$\abs{\cbr{1}} \gt \abs \varnothing$ になって反例になるから
こういう状況は取り除かないと
$B \neq \varnothing$ なる有限集合 $A, B$ に対し、
$A$ から $B$ への全射が存在しない ${}\implies{}$ $\abs A \lt \abs B$
$n = \abs A$ および $m = \abs B$ とする。$B \neq \varnothing$ より $m \geq 1$ である。 対偶を示す。つまり $n \geq m$ を仮定し、$A$ から $B$ への全射を構成する。
全単射 $g_A: [n] \rightarrow A$ と $g_B: [m] \rightarrow B$ を取り、写像 $h: [n] \rightarrow [m]$ を $$h(i) = \begin{cases} i & (\text{$i \in [m]$ のとき})\\ 1 & (\text{$i \not\in [m]$ のとき})\\ \end{cases}$$ で定義する。$m \geq 1$ なので $1 \in [m]$ であることに注意。$h$ は全射であり、よって $$g_B \circ h \circ g_A^{-1}: A \rightarrow B$$ も全射である。
次が言える
$B \neq \varnothing$ なる有限集合 $A, B$ に対し、
$\abs A \geq \abs B$ $~\iff~$ $A$ から $B$ への全射が存在する
$A \neq \varnothing$ かつ $B = \varnothing$ のとき、$\abs A \geq \abs B$ であるが $A$ から $B$ への全射は存在しない。