ベルンシュタインの定理の証明｜証明のイメージ付き
今日の目標
ベルンシュタインの定理を示す。
この記事で使う記号や用語
- 写像 $f: X \rightarrow Y$ に対し、$X$ の部分集合 $A$ の $f$ による像を $f(A)$ と書く。
ベルンシュタインの定理
単射と全射の間にはこんな関係があったよね
命題
空でない集合 $X$ と集合 $Y$ に対し、
$X$ から $Y$ への単射が存在する$\quad$ ならば $\quad$ $Y$ から $X$ への全射が存在する。
https://sorai-note.com/math/injection-surjection/
だからもし
$X$ から $Y$ への単射も $Y$ から $X$ への単射も
存在したら
$X$ から $Y$ への全射も $Y$ から $X$ への全射も
存在するけど……
$X$ から $Y$ への単射も $Y$ から $X$ への単射も
存在したら
$X$ から $Y$ への全射も $Y$ から $X$ への全射も
存在するけど……
このとき $X$ から $Y$ への全単射はあるの？
っていう疑問が湧く
っていう疑問が湧く
ありそうな感じだけどね
そう ある
あるんだけど示すのが意外と厄介
あるんだけど示すのが意外と厄介
今日示すのはこれ
ベルンシュタインの定理
集合 $X, Y$ に対し、
$X$ から $Y$ への単射が存在する $\quad$ かつ $\quad$ $Y$ から $X$ への単射が存在する
ならば $X$ から $Y$ への全単射が存在する。
ベルンシュタインの定理の証明のイメージ
さてどうしようか
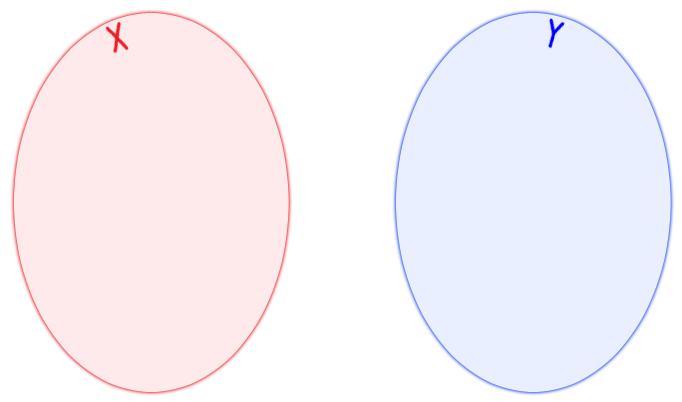
とりあえず
単射 $f: X \rightarrow Y$ と
単射 $g: Y \rightarrow X$ をとって……
単射 $f: X \rightarrow Y$ と
単射 $g: Y \rightarrow X$ をとって……
$X, Y$ をそれぞれ写してみようか
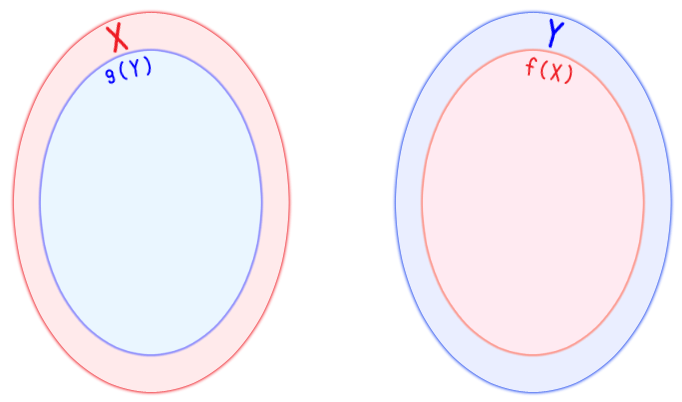
もっかい写そうか
$g(Y)$ を $f$ で写すと……
$f(g(Y))$ はどこにある？
$X \supseteq g(Y)$ だから
$f(X) \supseteq f(g(Y))$ だね
$f(X) \supseteq f(g(Y))$ だね
一方 $Y \supseteq f(X)$ だから
$g(Y) \supseteq g(f(X))$ もわかる
$g(Y) \supseteq g(f(X))$ もわかる
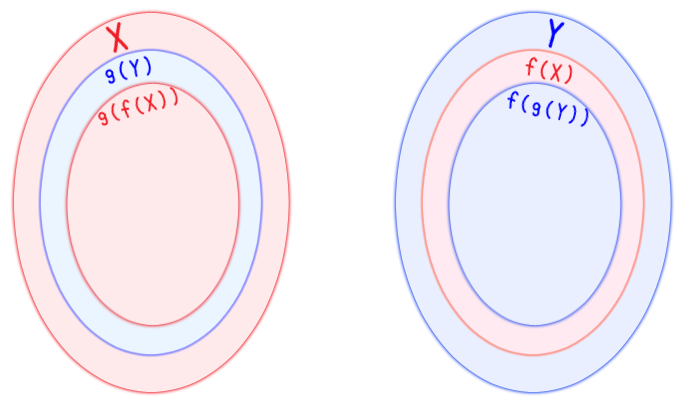
同じようにして……
$g(Y) \supseteq g(f(X))$ から $f(g(Y)) \supseteq f(g(f(X)))$ が出るし
$f(X) \supseteq f(g(Y))$ から $g(f(X)) \supseteq g(f(g(Y)))$ が出る
$g(Y) \supseteq g(f(X))$ から $f(g(Y)) \supseteq f(g(f(X)))$ が出るし
$f(X) \supseteq f(g(Y))$ から $g(f(X)) \supseteq g(f(g(Y)))$ が出る
永遠に繰り返せるね これ
単調に縮小しつづける包含関係の無限列ができるね
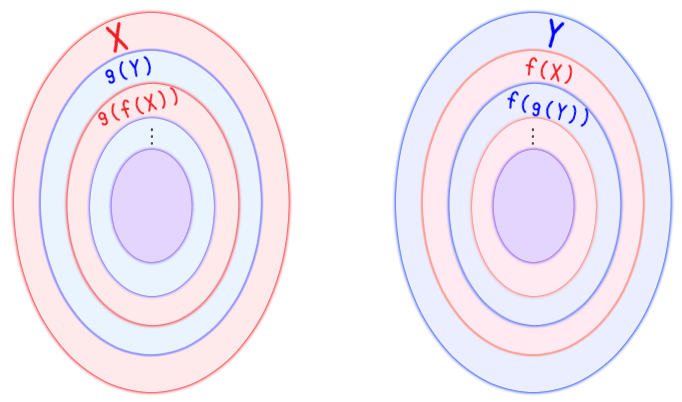
この紫の領域は？
どれだけ縮小していってもたどりつけない領域
包含関係の無限列の全ての共通部分って言った方がいいか
で 今の目的は全単射 $h: X \rightarrow Y$ を作ること
$X$ から $Y$ への写像……
ぱっと目に付くのは……
ぱっと目に付くのは……
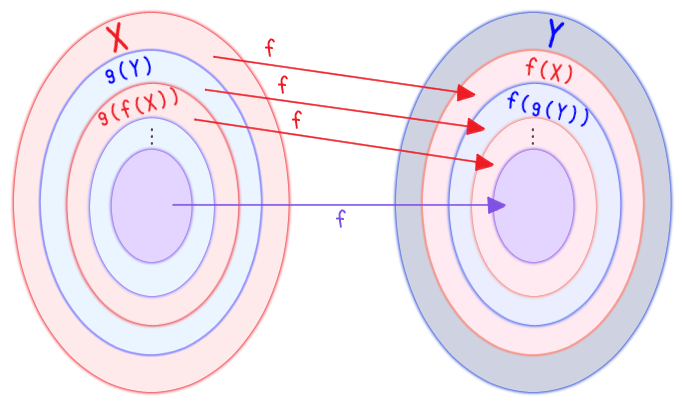
いや これじゃだめだわ
$Y \setminus f(X)$ が値域に入らない
$Y \setminus f(X)$ が値域に入らない
……あ
これでいけそうかな？
いいね
ベルンシュタインの定理の証明
