ε-N論法の演習問題 16 問(解答付き)|数列の極限
ε-N 論法に慣れる。演習問題で証明を書けるようになる。
- $\NN$ を非負整数全体の集合とする。
定義の確認
実数列 $\cbr{a_n}_{n \in \NN}$ が実数 $\alpha$ に収束するとは、
任意の正実数 $\varepsilon$ に対し、ある自然数 $N$ が存在して、
$\qquad$$\qquad$
$\qquad$$\qquad$
$n \geq N$ なる各自然数 $n$ に対し、$\abs{a_n \minus \alpha} \lt \varepsilon$
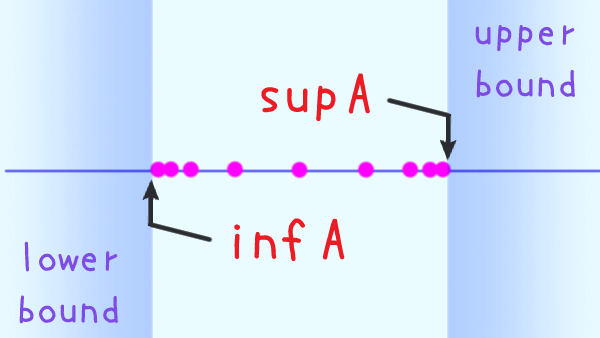
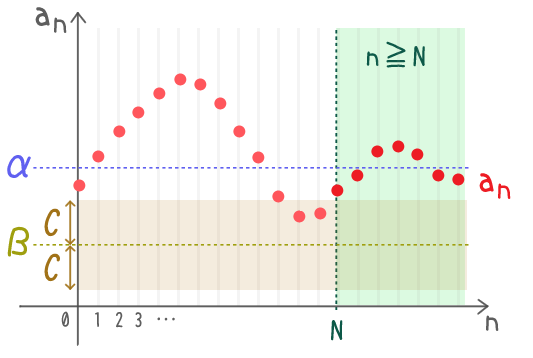
数列の収束のイメージ
$\alpha \minus \varepsilon \lt a_n \lt \alpha + \varepsilon$
$a_n$ が入ってるってこと
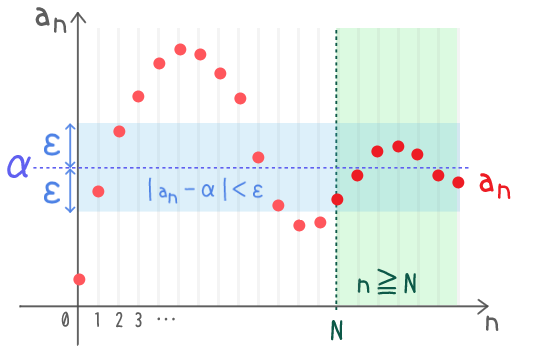
どんなに細く取ったとしても
$n$ がある自然数以上になったら
$a_n$ が常にその青い帯に入り続けるってこと
青い帯を更に細くしても
緑の領域を十分右にもっていけば
「緑の中の赤点は必ず青い帯に入る」状態に持っていける
ってことか
概念としてはそれだけなんだよね
いっぱい練習しよう
【LEVEL 1】具体的な数列の極限を ε-N 論法で示す
$\forall \varepsilon \gt 0, \exists N \in \NN, \forall n \geq N, \abs{\dfrac{n}{n+2} \minus 1} \lt \varepsilon$
を示す
量化子 0 個の式からはじめて
ちょっとずつ慣れていこう
$n \geq 3$ なる各自然数 $n$ に対し $\abs{\dfrac{n}{n + 2} \minus 1} \lt \dfrac{1}{2}$ であることを示せ。
$n \geq 3$ を任意に取る。このとき \begin{align} \abs{\dfrac{n}{n + 2} \minus 1} = \dfrac{2}{n + 2} \leq \dfrac{2}{5} \lt \dfrac{1}{2} \end{align}
$\dfrac{n}{n + 2}$ と $1$ の差は $\dfrac{1}{2}$ より小
前問を知らない体で解いてみよう
ある自然数 $N$ が存在して、$n \geq N$ なる各自然数 $n$ に対し $$\abs{\dfrac{n}{n + 2} \minus 1} \lt \frac{1}{2}$$ であることを示せ。
各自然数 $n$ に対し、 \begin{align} \abs{\dfrac{n}{n + 2} \minus 1} \lt \dfrac{1}{2} &\iff \dfrac{2}{n + 2} \lt \dfrac{1}{2} \\&\iff 4 \lt n + 2 \\&\iff n \gt 2 \end{align} となる。よって $n \geq 3$ ならば $\abs{\dfrac{n}{n + 2} \minus 1} \lt \dfrac{1}{2}$ が成り立つ。
不等式成立のためにどんな $N$ を取ればいいかを
探るって感じか
右辺の $\dfrac{1}{2}$ をもっと小さくしても成り立つかな?
ある自然数 $N$ が存在して、$n \geq N$ なる各自然数 $n$ に対し $$\abs{\dfrac{n}{n + 2} \minus 1} \lt \frac{1}{1000}$$ であることを示せ。
各自然数 $n$ に対し、 \begin{align} \abs{\dfrac{n}{n + 2} \minus 1} \lt \dfrac{1}{1000} &\iff \dfrac{2}{n + 2} \lt \dfrac{1}{1000} \\&\iff 2000 \lt n + 2 \\&\iff n \gt 1998 \end{align} となる。よって $n \geq 1999$ ならば $\abs{\dfrac{n}{n + 2} \minus 1} \lt \dfrac{1}{1000}$ が成り立つ。
任意の $\varepsilon \gt 0$ に対しある自然数 $N \in \NN$ が存在して、$n \geq N$ なる各自然数 $n$ に対し $$\abs{\dfrac{n}{n + 2} \minus 1} \lt \varepsilon$$ であることを示せ。すなわち ${\dfrac{n}{n + 2}} \rightarrow 1 \ (n \rightarrow \infty)$ を示せ。
$\varepsilon \gt 0$ を任意に取り固定する。 各自然数 $n$ に対し、 \begin{align} \abs{\dfrac{n}{n + 2} \minus 1} \lt \varepsilon &\iff \dfrac{2}{n + 2} \lt \varepsilon \\&\iff \dfrac{2}{\varepsilon} \lt n + 2 \\&\iff n \gt \dfrac{2}{\varepsilon} \minus 2 \end{align} となる。ここで $\dfrac{2}{\varepsilon} \minus 2$ より大きな自然数を一つ取って $N$ とする(※)。このとき $n \geq N$ ならば $n \gt \dfrac{2}{\varepsilon} \minus 2$ であり、上記の同値変形より $\abs{\dfrac{n}{n + 2} \minus 1} \lt \varepsilon$ となる。
この $N$ を明示したいときは $$N = \max \cbr{0, \left\lceil{\dfrac{2}{\varepsilon} \minus 2}\right\rceil}$$ ってすればいいね
例えば $\varepsilon = 2$ のとき
$N = \minus 1$ で自然数じゃなくなっちゃうから
(1) $\varepsilon \gt 0$ を固定する
(2) 一般の自然数 $n$ を用いて不等式を変形する
(3) $n$ がどんな値以上ならその不等式が成り立つのかを探る
っていう考え方で基本解けばいいのかな
$\varepsilon \gt 0$ を固定したあと
先の展開を予測してさっさと $N$ を明示して
$n \geq N$ として不等式を導出
っていう解答を書いてもいいかもね
$\dfrac{1}{n} \rightarrow 0 \ (n \rightarrow \infty)$ を示せ。
$\varepsilon \gt 0$ を任意に取る。このとき各自然数 $n$ に対し \begin{align} \abs{\dfrac{1}{n} \minus 0} \lt \varepsilon &\iff \dfrac{1}{n} \lt \varepsilon \\&\iff n \gt \dfrac{1}{\varepsilon} \end{align} となる。ここで $\dfrac{1}{\varepsilon}$ より大きな自然数を一つ取り $N$ とすると、$n \geq N$ ならば $n \gt \dfrac{1}{\varepsilon}$ であり $\abs{\dfrac{1}{n} \minus 0} \lt \varepsilon$ が成り立つ。
$\dfrac{n^2 + 1}{n^3} \rightarrow 0 \ (n \rightarrow \infty)$ を示せ。
$\varepsilon \gt 0$ を任意に取る。このとき各自然数 $n$ に対し \begin{align} \abs{\dfrac{n^2 + 1}{n^3} \minus 0} \lt \varepsilon &\iff \dfrac{n^2 + 1}{n^3} \lt \varepsilon \\&\iff n^2 + 1 \lt \varepsilon n^3 \\&\iff n^2(\varepsilon n \minus 1) \gt 1 \end{align} となる。$n \geq 1$ かつ $\varepsilon n\minus 1 \geq 2$ ならばこの不等式が成り立つことに注意。つまり
$n \geq 1$ かつ $n \geq \dfrac{3}{\varepsilon}$
ならばこの不等式が成り立つ。そこで $1$ よりも $\dfrac{3}{\varepsilon}$ よりも大きな自然数を一つ取って $N$ とすると、 各 $n \geq N$ に対し $\abs{\dfrac{n^2 + 1}{n^3} \minus 0} \lt \varepsilon$ が成り立つ。$N$ の取り方が雑だなー って思うかもだけど
慣れないうちはこれくらい雑に大きく取ってもいいと思う
$-1 \lt r \lt 1$ のとき $r^n \rightarrow 0 \ (n \rightarrow \infty)$ を示せ。
$r = 0$ のときは自明。$r \neq 0$ とする。つまり $0 \lt \abs{r} \lt 1$ である。
$\varepsilon \gt 0$ を任意に取る。$\abs{r} = \dfrac{1}{R}$ と書くと $R \gt 1$ なので $R = 1 + d$ ($d \gt 0$)と書ける。 このとき \begin{align} \abs{r^n} \lt \varepsilon &\iff \dfrac{1}{(1+d)^n} \lt \varepsilon \end{align} である。$n \geq 1$ のとき $\dfrac{1}{(1+d)^n} \leq \dfrac{1}{nd}$ であることに注意。よって $\dfrac{1}{Nd} \lt \varepsilon$ となる正整数 $N$ を一つ取ると
各 $n \geq N$ に対し $\dfrac{1}{(1+d)^n} \leq \dfrac{1}{nd} \leq \dfrac{1}{Nd} \lt \varepsilon$
すなわち $\abs{r^n} \lt \varepsilon$ である。【LEVEL 2】数列の収束を「使う」
実数 $x, y, z$ に対し
(1)
$x \leq \abs{x}$ および $-x \leq \abs{x}$ に注意。
$x + y \geq 0$ のときは $\abs{x + y} = x + y \leq \abs{x} + \abs{y}$ である。
$x + y \lt 0$ のときは $\abs{x + y} = \minus x \minus y \leq \abs{x} + \abs{y}$ である。
(2)
$\abs{x} = \abs{x + y \minus y} \leq \abs{x + y} + \abs{-y} = \abs{x + y} + \abs{y}$ から従う。
(2′)
$\abs{x + y} = \abs{y + x} \geq \abs{y} \minus \abs{x}$
(2")
(2) と (2′) から従う。
こんなのあったなっていうのを頭の片隅に置いといて
いっぱい問題解きながら慣れていこう
$\abs{x} \geq \abs{x \minus y} \minus \abs{2x \minus y}$ とか
$\abs{x \minus y} \leq \abs{x \minus z} + \abs{y \minus z}$ とか
$\abs{x \minus y} \geq \abs{\abs{x \minus 2y} \minus \abs{y}}$ とか
いろいろできるね
$\alpha = \beta$ ってことか
好き勝手に正実数 $r$ を選んで
「各 $n\geq N$ に対し $\abs{a_n \minus \alpha} \lt r$ 」
が成り立つような自然数 $N$ を取ってこれる
実数列が収束すれば一意であることを示せ。
実数列 $\cbr{a_n}_{n \in \NN}$ と実数 $\alpha, \beta$ に対し
$a_n \rightarrow \alpha \ (n \rightarrow \infty)$ $\quad$ かつ $\quad$ $a_n \rightarrow \beta \ (n \rightarrow \infty)$
と仮定する。$\varepsilon \gt 0$ を任意に取る。このとき、ある自然数 $N_1$ が存在して各 $n \geq N_1$ に対し $\abs{a_n \minus \alpha} \lt \varepsilon$
であり、ある自然数 $N_2$ が存在して各 $n \geq N_1$ に対し $\abs{a_n \minus \beta} \lt \varepsilon$
である。よって $N = \max\cbr{N_1, N_2}$ とすると$\abs{\alpha \minus \beta} \leq \abs{a_N \minus \alpha} + \abs{a_N \minus \beta} \lt 2\varepsilon$
である。「任意の $\varepsilon \gt 0$ に対し $\abs{\alpha \minus \beta} \lt 2\varepsilon$」が得られたので $$\abs{\alpha \minus \beta} \leq \inf_{\varepsilon \gt 0} (2 \varepsilon)$$ であり、右辺は $0$ なので $\abs{\alpha \minus \beta} = 0$ すなわち $\alpha = \beta$ である。実数列 $\cbr{a_n}_{n \in \NN}$ が実数 $\alpha$ に収束するとき $\ds\lim_{n \rightarrow \infty} a_n = \alpha$ と書く。
$\ds\lim_{n \rightarrow \infty} (a_n + b_n) = \alpha + \beta$ になることを示そう
実数列 $\cbr{a_n}_{n \in \NN}, \cbr{b_n}_{n \in \NN}$ と実数 $\alpha, \beta$ に対し、 $\ds\lim_{n \rightarrow \infty}a_n = \alpha$ かつ $\ds\lim_{n \rightarrow \infty}b_n = \beta$ ならば $$\ds\lim_{n \rightarrow \infty}(a_n + b_n) = \alpha + \beta$$ が成り立つことを示せ。
$\varepsilon \gt 0$ を任意に取る。各自然数 $n$ に対し \begin{align} \abs{(a_n + b_n) \minus (\alpha + \beta)} &= \abs{(a_n \minus \alpha) + (b_n \minus \beta)} \\&\leq \abs{a_n \minus \alpha} + \abs{b_n \minus \beta} \end{align} であることに注意。 $\ds\lim_{n \rightarrow \infty}a_n = \alpha$ と $\ds\lim_{n \rightarrow \infty}b_n = \beta$ より、ある自然数 $N_1, N_2$ が存在して、
各 $n \geq N_1$ に対し $\abs{a_n \minus \alpha} \lt \dfrac{\varepsilon}{2}$
各 $n \geq N_2$ に対し $\abs{b_n \minus \beta} \lt \dfrac{\varepsilon}{2}$
となる。よって $N = \max\cbr{N_1, N_2}$ とすると、各 $n \geq N$ に対して $$\abs{(a_n + b_n) \minus (\alpha + \beta)} \leq \dfrac{\varepsilon}{2}+\dfrac{\varepsilon}{2} \lt \varepsilon$$ となる。$\ds\lim_{n \rightarrow \infty} a_n b_n = \alpha \beta$ になることを示そう
実数列 $\cbr{a_n}_{n \in \NN}, \cbr{b_n}_{n \in \NN}$ と実数 $\alpha, \beta$ に対し、 $\ds\lim_{n \rightarrow \infty}a_n = \alpha$ かつ $\ds\lim_{n \rightarrow \infty}b_n = \beta$ ならば $$\ds\lim_{n \rightarrow \infty}a_n b_n = \alpha \beta$$ が成り立つことを示せ。
$\varepsilon \gt 0$ を任意に取る。各自然数 $n$ に対し \begin{align} \abs{a_n b_n \minus \alpha \beta} &= \abs{(a_n \minus \alpha)b_n + \alpha b_n \minus \alpha \beta} \\&= \abs{(a_n \minus \alpha)b_n + \alpha(b_n \minus \beta)} \\&\leq \abs{a_n \minus \alpha}\abs{b_n} + \abs{\alpha}\abs{b_n \minus \beta} \\&= \abs{a_n \minus \alpha}\abs{b_n \minus \beta + \beta} + \abs{\alpha}\abs{b_n \minus \beta} \\&\leq \abs{a_n \minus \alpha}\abs{b_n \minus \beta}\abs{\beta} + \abs{\alpha}\abs{b_n \minus \beta} \end{align} であることに注意。$\ds\lim_{n \rightarrow \infty}a_n = \alpha$ と $\ds\lim_{n \rightarrow \infty}b_n = \beta$ より、ある自然数 $N_1, N_2, N_3$ が存在して、
$\qquad$$\qquad$ 各 $n \geq N_1$ に対し $\abs{a_n \minus \alpha} \lt 1$
$\qquad$$\qquad$ 各 $n \geq N_2$ に対し $\abs{b_n \minus \beta} \lt \dfrac{\varepsilon}{2}\dfrac{1}{\abs{\beta} + 1}$ (※)
$\qquad$$\qquad$ 各 $n \geq N_3$ に対し $\abs{b_n \minus \beta} \lt \dfrac{\varepsilon}{2}\dfrac{1}{\abs{\alpha} + 1}$
となる。よって $n \geq \max\cbr{N_1, N_2, N_3}$ ならば \begin{align} \abs{a_n b_n \minus \alpha \beta} &\lt 1 \cdot \dfrac{\varepsilon}{2}\dfrac{1}{\abs{\beta} + 1}\cdot \abs{\beta} + \abs{\alpha} \cdot \dfrac{\varepsilon}{2}\dfrac{1}{\abs{\alpha} + 1} \\&\lt \dfrac{\varepsilon}{2} + \dfrac{\varepsilon}{2} \\&= \varepsilon \end{align} が成り立つ。ほんとは $\abs{b_n \minus \beta} \lt \dfrac{\varepsilon}{2}\dfrac{1}{\abs{\beta}}$ ってしたいところだけど
$\abs{\beta} = 0$ の可能性があったから
分母に +1 して回避
いろんな技術を学ぶともっとすっきり書けるよ
収束する実数列は有界であることを示せ。
※ここで実数列 $\cbr{a_n}_{n \in \NN}$ が有界であるとは、各 $n \in \NN$ に対し $\abs{a_n} \leq M$ となるような($n$ に依らない)定数 $M$ が存在することである。
実数列 $\cbr{a_n}_{n \in \NN}$ が実数 $\alpha$ に収束するとする。このときある自然数 $N$ が存在して
各 $n \geq N$ に対し $\abs{a_n \minus \alpha} \lt 1$
となる。よって各 $n \geq N$ に対し \begin{align} \abs{a_n} &\leq \abs{a_n \minus \alpha} + \abs{\alpha} \lt 1 + \abs{\alpha} \end{align} となる。よって全ての自然数 $n$ に対し $$\abs{a_n} \leq \max\cbr{\abs{a_0}, \ldots, \abs{a_{N \minus 1}}, 1 + \abs{\alpha}} $$ となり、右辺は $n$ に依らない定数。実数列 $\cbr{a_n}_{n \in \NN}, \cbr{b_n}_{n \in \NN}$ と実数 $\alpha, \beta$ に対し、 $\ds\lim_{n \rightarrow \infty}a_n = \alpha$ かつ $\ds\lim_{n \rightarrow \infty}b_n = \beta$ ならば $$\ds\lim_{n \rightarrow \infty}a_n b_n = \alpha \beta$$ が成り立つことを示せ。
$\varepsilon \gt 0$ を任意に取る。各自然数 $n$ に対し \begin{align} \abs{a_n b_n \minus \alpha \beta} &= \abs{(a_n \minus \alpha)b_n + \alpha b_n \minus \alpha \beta} \\&= \abs{(a_n \minus \alpha)b_n + \alpha(b_n \minus \beta)} \\&\leq \abs{a_n \minus \alpha}\abs{b_n} + \abs{\alpha}\abs{b_n \minus \beta} \end{align} であることに注意。 収束列は有界なので、$\abs{b_n} \leq M$ なる定数 $M$ が存在する。$M \gt 0$ としてよい。また $\ds\lim_{n \rightarrow \infty}a_n = \alpha$ と $\ds\lim_{n \rightarrow \infty}b_n = \beta$ より、ある自然数 $N_1, N_2$ が存在して、
各 $n \geq N_1$ に対し $\abs{a_n \minus \alpha} \lt \dfrac{\varepsilon}{2}\dfrac{1}{M}$ (※)
各 $n \geq N_2$ に対し $\abs{b_n \minus \beta} \lt \dfrac{\varepsilon}{2}\dfrac{1}{\abs{\alpha} + 1}$ (※)
である。よって $n \geq \max\cbr{N_1, N_2}$ ならば \begin{align} \abs{a_n b_n \minus \alpha \beta} &\lt \dfrac{\varepsilon}{2}\dfrac{M}{M} + \dfrac{\varepsilon}{2}\dfrac{\abs{\alpha}}{\abs{\alpha} + 1} \\&\lt \dfrac{\varepsilon}{2} + \dfrac{\varepsilon}{2} \\&= \varepsilon \end{align} が成り立つ。ちょっと解答がすっきりしたね
めんどくさいよね
【LEVEL 3】"$\lt \varepsilon$" にこだわらない
$\abs{a_n \minus \alpha} \lt \varepsilon$ を導出するのを目指してたけど……
$\abs{a_n \minus \alpha} \lt c\varepsilon$ を導出すれば十分
$\abs{a_n \minus \alpha} \lt c\varepsilon$ を示す代わりに
$\abs{a_n \minus \alpha} \leq c\varepsilon$ でもいい
$\exists N \in\NN, \forall n \geq N, \abs{a_n \minus \alpha} \leq c\varepsilon$
が導出できたとする……$\exists N \in\NN, \forall n \geq N, \abs{a_n \minus \alpha}\leq c\varepsilon$
が導出できたとする……$\exists N \in\NN, \forall n \geq N, \abs{a_n \minus \alpha} = 0 \lt \varepsilon’$
でオッケーだし$c \gt 0$ ならさっきと同じ方法でいい
実数列 $\cbr{a_n}_{n \in \NN}$ と実数 $\alpha$ に対し、以下は同値。
任意の正実数 $\varepsilon$ に対し、ある自然数 $N$ が存在して、
$n \geq N$ なる各自然数 $n$ に対し、$\abs{a_n \minus \alpha} \lt \varepsilon$
ある非負実数 $c$ が存在し、
任意の正実数 $\varepsilon$ に対し、ある自然数 $N$ が存在して、
$n \geq N$ なる各自然数 $n$ に対し、$\abs{a_n \minus \alpha} \leq c\varepsilon$
$c = 1$ とすればよい。
$c = 0$ のときは自明。$c \gt 0$ とする。$\varepsilon \gt 0$ を任意に取ると (II) よりある自然数 $N$ が存在して
各 $n \geq N$ に対し $\abs{a_n \minus \alpha} \leq c \cdot \dfrac{\varepsilon}{2c} = \dfrac{\varepsilon}{2} \lt \varepsilon$
となる。実数列 $\cbr{a_n}_{n \in \NN}, \cbr{b_n}_{n \in \NN}$ と実数 $\alpha, \beta$ に対し、 $\ds\lim_{n \rightarrow \infty}a_n = \alpha$ かつ $\ds\lim_{n \rightarrow \infty}b_n = \beta$ ならば $$\ds\lim_{n \rightarrow \infty}a_n b_n = \alpha \beta$$ が成り立つことを示せ。
$\varepsilon \gt 0$ を任意に取る。各自然数 $n$ に対し \begin{align} \abs{a_n b_n \minus \alpha \beta} &= \abs{(a_n \minus \alpha)b_n + \alpha b_n \minus \alpha \beta} \\&= \abs{(a_n \minus \alpha)b_n + \alpha(b_n \minus \beta)} \\&\leq \abs{a_n \minus \alpha}\abs{b_n} + \abs{\alpha}\abs{b_n \minus \beta} \end{align} であることに注意。収束列は有界なので、$\abs{b_n} \leq M$ なる定数 $M$ が存在する。また $\ds\lim_{n \rightarrow \infty}a_n = \alpha$ と $\ds\lim_{n \rightarrow \infty}b_n = \beta$ より、ある自然数 $N_1, N_2$ が存在して、
各 $n \geq N_1$ に対し $\abs{a_n \minus \alpha} \lt \varepsilon$
各 $n \geq N_2$ に対し $\abs{b_n \minus \beta} \lt \varepsilon$
である。よって $n \geq \max\cbr{N_1, N_2}$ ならば \begin{align} \abs{a_n b_n \minus \alpha \beta} &\lt \varepsilon M + \abs{\alpha} \varepsilon = (M + \abs{\alpha})\varepsilon \end{align} が成り立つ。適当に空気読んでね
数をこなせば自然に身に付くから
とにかくガンガン問題解こう
実数列 $\cbr{a_n}_{n \in \NN}$ と実数 $\alpha, c$ に対し、$\ds\lim_{n \rightarrow \infty}a_n = \alpha$ ならば $$\ds\lim_{n \rightarrow \infty} c a_n = c \alpha$$ であることを示せ。
$\varepsilon \gt 0$ を任意に取る。$\ds\lim_{n \rightarrow \infty}a_n = \alpha$ より、ある自然数 $N$ が存在して、
各 $n \geq N$ に対し $\abs{a_n \minus \alpha} \lt \varepsilon$
となる。このとき各 $n \geq N$ に対し $\abs{c a_n \minus c \alpha} = \abs{c}\abs{a_n \minus \alpha} \lt \abs{c}\varepsilon$ となる。実数列 $\cbr{a_n}_{n \in \NN}$ と実数 $\alpha$ に対し $\ds\lim_{n \rightarrow \infty}a_n = \alpha$ であるとする。以下を示せ。
(1)
$\beta \lt \alpha$ ならば、$\beta \lt \gamma \lt \alpha$ なる実数 $\gamma$ と自然数 $N$ で
各 $n \geq N$ に対し $\gamma \lt a_n$
となるものが存在する。(2)
$\alpha \lt \beta$ ならば、$\alpha \lt \gamma \lt \beta$ なる実数 $\gamma$ と自然数 $N$ で
各 $n \geq N$ に対し $a_n \lt \gamma$
となるものが存在する。(3)
$\alpha \neq \beta$ ならば、$0 \lt C \lt \abs{\alpha \minus \beta}$ なる実数 $C$ と自然数 $N$ で
各 $n \geq N$ に対し $\abs{a_n – \beta} \gt C$
となるものが存在する。
(1)
$\alpha \gt \beta$ と $\ds\lim_{n \rightarrow \infty}a_n = \alpha$ より、ある自然数 $N$ が存在して
各 $n \geq N$ に対し $\abs{a_n \minus \alpha} \lt \dfrac{\alpha \minus \beta}{2}$
であり、特にこのとき $\minus\dfrac{\alpha \minus \beta}{2} \lt a_n \minus \alpha$ なので各 $n \geq N$ に対し $a_n \gt \dfrac{\alpha + \beta}{2}$
であり、$\beta \lt \dfrac{\alpha + \beta}{2} \lt \alpha$ である。(2)
$\ds\lim_{n \rightarrow \infty}(\minus a_n) = \minus \alpha$ と $\minus \alpha \gt \minus \beta$ と (1) より、$\minus \beta \lt \gamma \lt \minus \alpha$ なる実数 $\gamma$ および自然数 $N$ が存在して
各 $n \geq N$ に対し $\gamma \lt \minus a_n$
となる。よって各 $n \geq N$ に対し $a_n \lt \minus \gamma$ であり、また $\alpha \lt \minus \gamma \lt \beta$ である。(3)
(1) が成り立つときは $C = \gamma \minus \beta$、(2) が成り立つときは $C = \beta \minus \gamma$ とすればよい。
実数列 $\cbr{a_n}_{n \in \NN}$ と実数 $\alpha \neq 0$ に対し、$\ds\lim_{n \rightarrow \infty}a_n = \alpha$ ならば $$\ds\lim_{n \rightarrow \infty}\dfrac{1}{a_n} = \dfrac{1}{\alpha}$$ が成り立つことを示せ。
$\varepsilon \gt 0$ を任意に取る。問題9より、ある正実数 $C$ と自然数 $N_1$ が存在して
各 $n \geq N_1$ に対し $\abs{a_n} \geq C$
となる。特に各 $n \geq N_1$ に対し $a_n \neq 0$ であることに注意。また $\ds\lim_{n \rightarrow \infty}a_n = \alpha$ より、ある自然数 $N_2$ が存在して
各 $n \geq N_2$ に対し $\abs{a_n \minus \alpha} \lt \varepsilon$
となる。よって $N = \max\cbr{N_1, N_2}$ とすると、各 $n \geq N$ に対し $$\abs{\dfrac{1}{a_n} \minus \dfrac{1}{\alpha}} = \dfrac{\abs{a_n \minus \alpha}}{\abs{a_n}\abs{\alpha}} \lt \dfrac{1}{C\abs{\alpha}}\varepsilon $$ である。実数列 $\cbr{a_n}_{n\in \NN},\cbr{b_n}_{n\in \NN}$ と実数 $\alpha, \beta$ に対し、 $\ds\lim_{n \rightarrow \infty} a_n = \alpha$ かつ $\ds\lim_{n \rightarrow \infty} b_n = \beta$ かつ
各自然数 $n$ に対し $a_n \leq b_n$ $\quad$(※)
ならば $\alpha \leq \beta$ であることを示せ。$\varepsilon, \delta \gt 0$ を任意に取る。このとき $\ds\lim_{n \rightarrow \infty} a_n = \alpha$ と $\ds\lim_{n \rightarrow \infty} b_n = \beta$ より、ある自然数 $N_1, N_2$ が存在して
各 $n \geq N_1$ に対し $\abs{a_n \minus \alpha} \lt \varepsilon$
各 $n \geq N_2$ に対し $\abs{b_n \minus \beta} \lt \delta$
となる。よって $N = \max\cbr{N_1, N_2}$ に対し$\alpha \minus \varepsilon \lt a_N$ $\quad$ かつ $\quad$ $b_N \lt \beta + \delta$
となり、更に $a_N \leq b_N$ より $\alpha \minus \varepsilon \lt \beta + \delta$ となる。任意の $\varepsilon, \delta \gt 0$ に対しこれが成り立つので $$\ds\sup_{\varepsilon \gt 0} (\alpha \minus \varepsilon) \leq \inf_{\delta \gt 0}(\beta + \delta)$$ となり $\alpha \leq \beta$ を得る。「無限個の $n$ に対して $a_n \leq b_n$」
ってしても ほとんど同じように証明できるね
$N$ が取れるからか
実数列 $\cbr{a_n}_{n\in \NN},\cbr{b_n}_{n\in \NN}, \cbr{c_n}_{n\in \NN}$ と実数 $\alpha$ に対し、 $\ds\lim_{n \rightarrow \infty} a_n = \ds\lim_{n \rightarrow \infty} c_n = \alpha$ かつ
各自然数 $n$ に対し $a_n \leq b_n \leq c_n$
ならば $\ds\lim_{n \rightarrow \infty} b_n = \alpha$ であることを示せ。$\varepsilon \gt 0$ を任意に取る。このときある自然数 $N_1, N_2$ が存在して
各 $n \geq N_1$ に対し $\abs{a_n \minus \alpha} \lt \varepsilon$
各 $n \geq N_2$ に対し $\abs{c_n \minus \alpha} \lt \varepsilon$
である。よって $n \geq \max \cbr{N_1, N_2}$ のとき $\alpha \minus \varepsilon \lt a_n$ かつ $c_n \lt \alpha + \varepsilon$ なので $$\alpha \minus \varepsilon \lt b_n \lt \alpha + \varepsilon$$ となり $\abs{b_n \minus \alpha} \lt \varepsilon$を得る。だるくなってきたな……
「ある自然数 $N$ が存在して 各 $n \geq N$ に対し
$\abs{a_n \minus \alpha} \lt \varepsilon$ かつ $\abs{c_n \minus \alpha} \lt \varepsilon$」
って書いちゃってもいいかもね
実数列 $\cbr{a_n}_{n\in \NN}$ と実数 $\alpha$ に対し、
$\ds\lim_{n \rightarrow \infty}a_n = \alpha$ $\quad$ ならば $\quad$ $\ds\lim_{n \rightarrow \infty}\frac{a_0 + \cdots + a_{n\minus 1}}{n} = \alpha$
であることを示せ。各自然数 $n$ に対し $$\frac{a_0 + \cdots + a_{n\minus 1}}{n} \minus \alpha = \frac{(a_0 \minus \alpha) + \cdots + (a_{n\minus 1} \minus \alpha)}{n}$$ なので、$\alpha = 0$ のときに示せば十分。
$\varepsilon \gt 0$ を任意に取る。$\ds\lim_{n\rightarrow \infty}a_n = 0$ なので、ある自然数 $N$ が存在して、
各 $n \geq N$ に対し $\abs{a_n} \lt \varepsilon$
である。$A_N = \max\cbr{\abs{a_1}, \ldots, \abs{a_{N \minus 1}}}$ とすると$\qquad$ 各 $n \geq N$ に対し \begin{align} &\abs{\frac{a_0 + \cdots + a_{n\minus 1}}{n}} \\ &\qquad\leq \dfrac{\abs{a_0} + \cdots + \abs{a_{N\minus 1}} + \abs{a_{N}} + \cdots + \abs{a_{n\minus 1}} }{n} \\ &\qquad\leq \dfrac{N A_N}{n} + \dfrac{n-N}{n}{\varepsilon} \\ &\qquad\lt \dfrac{N A_N}{n} + \varepsilon \end{align} となる。$\dfrac{N A_N}{M} \lt \varepsilon$ なる自然数 $M$ を取ると
各 $n \geq M$ に対し $\dfrac{N A_N}{n} \lt \varepsilon$
となるので、各 $n \geq \max\cbr{N, M}$ に対し $\abs{\dfrac{a_0 + \cdots + a_{n\minus 1}}{n}} \lt 2 \varepsilon$ となる。実数列 $\cbr{a_n}_{n \in \NN}$ と実数 $\alpha$ に対し、
$\ds\lim_{n \rightarrow \infty} {a_n} = \alpha$ ならば $\ds\lim_{n \rightarrow \infty} \abs{a_n} = \abs{\alpha}$
であることを示せ。$\varepsilon \gt 0$ を任意に取る。$\ds\lim_{n \rightarrow \infty} {a_n} = \alpha$ より、ある自然数 $N$ が存在して
各 $n \geq N$ に対し $\abs{a_n \minus \alpha} \lt \varepsilon$
となり、$\abs{\abs{a_n} \minus \abs{\alpha}} \leq \abs{a_n \minus \alpha}$ なので各 $n \geq N$ に対し $\abs{\abs{a_n} \minus \abs{\alpha}} \lt \varepsilon$
である。実数列 $\cbr{a_n}_{n \in \NN}$ と $\alpha \in (\minus 1, 1)$ に対し、
$\ds\lim_{n \rightarrow \infty} \dfrac{a_{n+1}}{a_n} = \alpha$ ならば $\ds\lim_{n \rightarrow \infty} a_n = 0$
であることを示せ。問題9より、$\minus 1 \lt \gamma_1 \lt \alpha \lt \gamma_2 \lt 1$ なる実数 $\gamma_1, \gamma_2$ および自然数 $N_1, N_2$ が存在して、
各 $n \geq N_1$ に対し $\dfrac{a_{n+1}}{a_n} \gt \gamma_1$
各 $n \geq N_2$ に対し $\dfrac{a_{n+1}}{a_n} \lt \gamma_2$
であり、$N = \max\cbr{N_1, N_2}$ および $r = \max\cbr{\abs{\gamma_1}, \abs{\gamma_2}}$ とすると $r \in [0, 1)$ で各 $n \geq N$ に対し $\minus r \leq \gamma_1 \lt \dfrac{a_{n+1}}{a_n} \lt \gamma_2 \leq r$
となる。よって各 $n \geq N$ に対し $\abs{a_{n+1}} \lt r \abs{a_n}$ なので各 $n \geq N$ に対し $\minus r^{n \minus N}\abs{a_{N}} \lt \abs{a_n} \lt r^{n \minus N}\abs{a_{N}}$
となり、$n \rightarrow \infty$ として $\ds\lim_{n \rightarrow \infty}{a_n} = 0$ を得る。整数列 $\cbr{a_n}_{n \in \NN}$ が収束すれば、ある自然数 $N$ が存在して
$a_{N} = a_{N+1} = a_{N+2} = \cdots$
であることを示せ。$\ds\lim_{n \rightarrow \infty} a_n = \alpha$ とする。このときある自然数 $N$ が存在して
各 $n \geq N$ に対し $\abs{a_n \minus \alpha} \lt \dfrac{1}{2}$
すなわち各 $n \geq N$ に対し $\alpha \minus \dfrac{1}{2} \lt a_n \lt \alpha + \dfrac{1}{2}$ である。長さ $1$ の開区間に属する整数は高々一つなので(※)、$a_N, a_{N+1}, a_{N+2}, \ldots$ は全て同じ整数である。もし $x \lt m_1 \lt m_2 \lt x + 1$ だとしたら
$0 \lt m_2 \minus m_1 \lt (x + 1) \minus x = 1$ より
$0$ と $1$ の間に整数が存在することになって矛盾