ツォルンの補題の証明
選択公理からツォルンの補題を示す。
以下、$X$ は集合で $\leq$ は $X$ 上の半順序とする。
基礎事項と用語の確認
$C \subseteq X$ が鎖であるとは、
各 $x, y \in C$ に対し $x \leq y$ または $y \leq x$
であることとする(つまり $C$ は $\leq$ により全順序集合)。
$S \subseteq X$ が整列集合であるとは、
$S$ の空でない部分集合は必ず最小元を持つ
こととする。
整列集合は鎖である。
整列集合 $S$ に対し $x, y \in S$ を任意に取ると、$S$ の非空部分集合 $\cbr{x, y}$ は最小元を持つので $x \leq y$ または $y \leq x$ である。
$x, y \in X$ に対し $x \lt y$ とは
$x \leq y$ かつ $x \neq y$
であることとして定める。
整列集合 $S \subseteq X$ と $a \in S$ に対し、整列集合 $S[a]$ を $$S[a] = \iset{b \in S}{b \lt a}$$ で定め、$S$ の $a$ による切片という。
-
$x \in X$ が極大元であるとは
各 $y \in X$ に対し $x \not\lt y$
であることとする。
-
$u \in X$ が $A \subseteq X$ の上界であるとは
各 $a \in A$ に対し $a \leq u$
であることとする。
-
$v \in X$ が $A \subseteq X$ の強上界であるとは
各 $a \in A$ に対し $a \lt v$
であることとする。
選択公理を仮定する。このとき $X$ の任意の鎖が上界を持つならば $X$ は極大元を持つ。
「極大元がない $\implies$ 上界を持たない鎖がある」
を示す
極大元が存在しない状況では
上界の存在と強上界の存在は同値
$X$ は極大元を持たないとする。このとき $X$ の部分集合が上界を持つことと強上界を持つことは同値である。
強上界は上界なので、強上界を持てば上界を持つ。
逆に $A$ が上界 $u$ を持つと、$u$ は極大元でないので $u \lt v$ なる $v$ が存在し、
各 $a \in A$ に対し $a \leq u \lt v$
となるので $v$ が $A$ の強上界になる。
強上界を持つ整列集合は延長できる
ってことも確認しとこう
整列集合 $S \subseteq X$ が強上界 $v$ を持てば $S \cup \cbr{v}$ も整列集合である。
$S \cup \cbr{v}$ の非空部分集合 $A$ を任意に取り、$A$ が最小元を持つことを示す。
$A = \cbr{v}$ のときや $A \subseteq S$ のときは自明。そうでないとき $$A = (A \cap S) \cup \cbr{v}$$ であり、$A \cap S$ が $S$ の非空部分集合なので $m = \min(A \cap S)$ が存在するが、
各 $a \in A \cap S$ に対し $a \lt v$
なので、$A$ の最小元は $m$ である。
「整列集合の延長」を考えるときに
しっくりくるからね
強上界を持たない整列集合を作るのを目指すよ
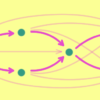
ツォルンの補題の証明のイメージ
けっこうでかい整列集合を作るってこと?
整列集合をたくさん集めて
その和集合を取ろうかと
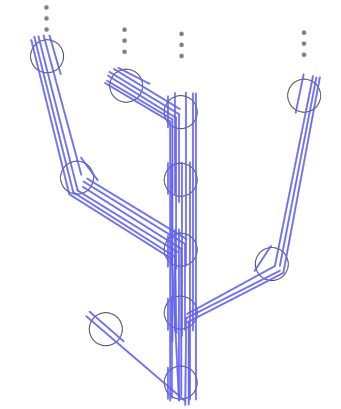
青線はそれぞれ整列集合だと思ってね
こんな感じの整列集合の集まりを取り出したい
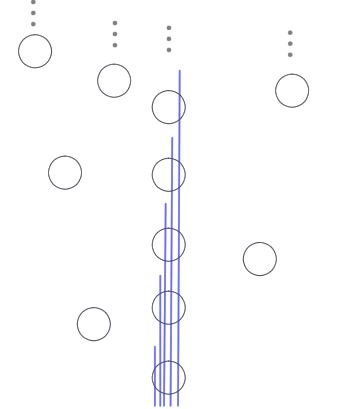
選択公理を使うよ
その強上界を一つずつ選んでくれるような
関数 $f$ を選択公理で取ってくる
整列集合だけを集めて $\mathcal{S}_f$ を作る
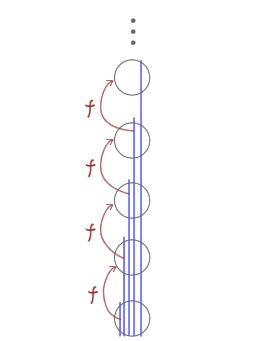
$S \cup \cbr{f(S)} \in \mathcal{S}_f$」ってことを示して……
$\tilde{S} \cup \cbr{f(\tilde{S})}$ っていうもっとでかいのが作れて
でも $\tilde{S}$ は $\mathcal{S}_f$ の中で一番でかいはずだから
それはおかしいねってことね
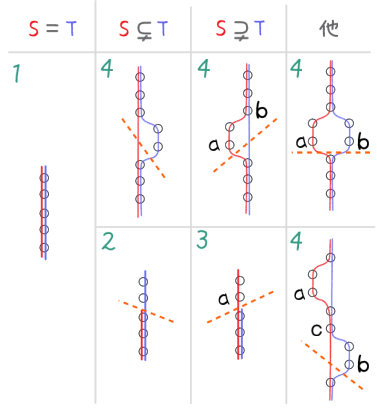
ふたつの整列集合を「切って」同じにする
便利なのがこれ
整列集合 $S, T \subseteq X$ に対し、
- $S = T$
- $S = T[b]$ となる $b \in T$ が存在する
- $S[a] = T$ となる $a \in S$ が存在する
- $S[a] = T[b]$ かつ $a \neq b$ となる $a \in S$ と $b \in T$ が存在する
のいずれかが成立する。
1 ~ 3 が成り立たないとして 4 を示す。1 でないので 「$S \not\subseteq T$ または $T \not\subseteq S$」 だが、対称性より $S \not\subseteq T$ としてよい。
$S \setminus T$ が非空なので $$a = \min(S \setminus T)$$ が存在する。最小性から、$a$ より小さな要素は $S \setminus T$ に属さない。つまり $$S[a] \subseteq T$$ である。いま 3 は成り立たないので $S[a] \not\supseteq T$ である。よって $$b = \min(T \setminus S[a])$$ が存在し、最小性から $$T[b] \subseteq S[a]$$ である。ここで $a \neq b$ であることが $a \not\in T$ と $b \in T$ からわかる。 よってもし $T[b] \supseteq S[a]$ であれば 4 が成り立つことがわかる。
以下 $T[b] \not\supseteq S[a]$ とする。このとき $$c = \min(S[a] \setminus T[b])$$ が存在し、最小性から $S[a][c] \subseteq T[b]$ だが、$c \in S[a]$ なので $$S[c] \subseteq T[b]$$ である。ここで $b \neq c$ であることが $b \not\in S[a]$ と $c \in S[a]$ からわかる。
$b \lt c$ を示す。 $c \in T$ であることが $c \in S[a]$ からわかる。更に $c \not\lt b$ であることが $c \not\in T[b]$ からわかる。$b$ も $c$ も鎖 $T$ に属し $b = c$ でも $c \lt b$ でもないので、$b \lt c$ になるしかない。
$T[b] \subseteq S[a]$ より $T[b]$ の要素は $S$ に属すことと $b \lt c$ であることにより $$T[b] \subseteq S[c]$$ となり、$T[b] = S[c]$ を得た。よって 4 が成り立つ。
ツォルンの補題の証明
選択公理を仮定する。このとき $X$ の任意の鎖が上界を持つならば $X$ は極大元を持つ。
$X$ に極大元がないと仮定し、上界を持たない鎖が存在することを示す。このとき $X$ の部分集合が上界を持つことと強上界を持つことが同値になることに注意(命題2)。
強上界を持つ鎖全体(したがって上界を持つ鎖全体)を $\hat{\mathcal{C}}$ とする。このとき選択公理より
各 $C \in \hat{\mathcal{C}}$ に対し $f(C)$ は $C$ の強上界
であるような写像 $f: \hat{\mathcal{C}} \rightarrow X$ が存在する。ここで整列集合 $S \subseteq X$ で $$\forall a \in S, f(S[a]) = a$$ なるもの全体を $\mathcal{S}_f$ と書く($S[a]$ は強上界 $a$ を持つので $S[a] \in \hat{\mathcal{C}}$)。
$S, T \in \mathcal{S}_f$ で $S \neq T$ ならば
「$S$ は $T$ のある切片」 または 「$T$ は $S$ のある切片」
となる。特に $S, T \in \mathcal{S}_f$ に対し $S \subseteq T$ または $T \subseteq S$ である。
もし $S[a] = T[b]$ となる $a \in S, b \in T$ が存在したら $$a = f(S[a]) = f(T[b]) = b$$ なので 定理4の 4 は $S, T \in \mathcal{S}_f$ に対して成り立たない。 いま定理4の 1 も成り立たないので、一方がもう一方の切片になるしかない。
$\displaystyle \tilde{S}$$\displaystyle{} = \bigcup_{S \in \mathcal{S}_f} S$ とする。
$\displaystyle \tilde{S}$ は鎖である。
$a, b \in \tilde{S}$ とすると $a \in S, b \in T$ なる $S, T \in \mathcal{S}_f$ が取れ、主張1より
$S \subseteq T$ または $T \subseteq S$
である。よって $a, b \in T$ または $a, b \in S$ であり、$S$ も $T$ も鎖なので、どちらの場合でも「$a \leq b$ または $a \geq b$」を得る。
$a, b \in \tilde{S}$ で $a \lt b$ のとき、任意の $S \in \mathcal{S}_f$ に対し $$b \in S \implies a \in S$$ が成り立つ。
$b \in S$ とし、$a \in T$ なる $T \in \mathcal{S}_f$ を取る。 主張1を用いる。まず $$S[c] = T \qquad (c \in S)$$ のときは $a \in T = S[c] \subseteq S$ である。一方 $$S = T[c] \qquad (c \in T)$$ のときは $a \lt b$ と $b \in S = T[c]$ より $a \in T[c] = S$ である。
$\displaystyle \tilde{S}$ は整列集合である。
$A$ が $\tilde{S}$ の非空部分集合ならば、$\tilde{S}$ の定義より $A \cap S \neq \varnothing$ なる $S \in \mathcal{S}_f$ が存在し、$S$ は整列集合なので $$m = \min(A \cap S)$$ が存在する。
$a \in A$ を任意に取る。もし $a \lt m$ ならば、主張3と $m \in S$ から $a \in S$ となり、$m$ の最小性に矛盾する。よって $a \not\lt m$ であり、主張2より $\tilde{S}$ は鎖なので $$m \leq a$$ であり $m = \min A$ を得る。
$\displaystyle \tilde{S} \in \mathcal{S}_f$ である。
主張4より $\tilde{S}$ は整列集合。$a \in \tilde{S}$ を任意に取って $f(\tilde{S}[a]) = a$ を示す。
$a \in S$ なる $S \in \mathcal{S}_f$ を取ると、$S \subseteq \tilde{S}$ より $$S[a] \subseteq \tilde{S}[a]$$ である。一方 $b \in \tilde{S}[a]$ を任意に取ると、$b \lt a$ と主張3と $a \in S$ より $b \in S$ であり、$b \in S[a]$ を得る。よって $$\tilde{S}[a] \subseteq {S}[a]$$ も得られた。したがって $\tilde{S}[a] = {S}[a]$ となり $$f(\tilde{S}[a]) = f({S}[a]) = a$$ である。
$S \in \mathcal{S}_f$ が強上界を持てば $S \cup \cbr{f(S)} \in \mathcal{S}_f$ である。
$f(S)$ は $S$ の強上界。$S’ = S \cup \cbr{f(S)}$ とすると命題3より $S’$ は整列集合なので、各 $a \in S’$ に対し $f(S'[a]) = a$ を示せばよい。
$a = f(S)$ のときは、 $$f(S'[a]) = f(S'[f(S)]) = f(S) = a$$ である。
$a \in S$ のときは、$a \lt f(S)$ なので $$S'[a] = S[a]$$ である。よって $f(S'[a]) = f(S[a]) = a$ を得る。
もし $\tilde{S}$ が上界を持てば強上界も持ち(命題2)、主張6より $$\tilde{S} \subsetneq \tilde{S} \cup \cbr{f(\tilde{S})} \in \mathcal{S}_f$$ となるが、これは $\tilde{S}$ の定義に反する。
よって鎖 $\tilde{S}$ は上界を持たない。
空集合に対するツォルンの補題
$X$ が空集合のときを除外してないけど
大丈夫?
$X$ の鎖は $\varnothing$ ただ一つでしょ
「任意の鎖が上界を持つならば」って言ってる時点で
$X \neq \varnothing$ になるのか