集合を使って「自然数」を作る｜ペアノの公理を満たすシステムの構成
集合でペアノシステムを構成する。
ペアノの公理とは
そこから自然数の基本的な性質が引き出せる
集合 $\NN$ とその要素 $0 \in \NN$ と写像 $s: \NN \rightarrow \NN$ の組 $(\NN, 0, s)$ で
$\NN$ の部分集合 $A$ が
を共に満たせば $A = \NN$
を満たすものをペアノシステムと呼ぶ。
$0$ は普通に $0$ で
$s(n)$ は $n+1$ に相当するものだっけか
ペアノシステムを構成するよ
自然数全体の集合 $\NN$ を構成する方法
集合 $X$ が帰納的とは2条件
を満たすことをいう。
そこで帰納的な集合の存在が仮定される
「次の集合」をこう定めると
なにかと都合がいい
$\varnothing$ の「次の集合」も持ってて
更にその「次の集合」も持ってて……
全然関係ない集合も持ってるかもしれない
★ の「次の集合」も持ってて
更にその「次の集合」も持ってて……
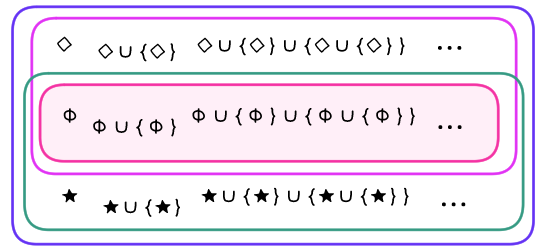
帰納的な集合の中で一番小さいものを
$\NN$ として定義したい
$X$ の部分集合で帰納的なもの全ての共通部分を
$\NN$ としたいところだけど……
帰納的な集合 $X$ に対し、$X$ の部分集合で帰納的な集合すべての共通部分を $\NN_X$ とする。
帰納的な集合 $X, Y$ に対し $\NN_X = \NN_Y$ が成り立つ。
対称性より $\NN_X \subseteq \NN_Y$ を示せば十分。$Y$ の部分集合で帰納的な集合 $A$ を任意に取って $$\NN_X \subseteq A$$ を示すことができれば、$\NN_Y$ の定義より $\NN_X \subseteq \NN_Y$ を帰結できる。
いま $A$ も $X$ も帰納的なので、$A \cap X$ も帰納的。この $A \cap X$ は $X$ の部分集合なので、$\NN_X$ の定義より $$\NN_X \subseteq A \cap X$$ であり、$A \cap X \subseteq A$ なので $\NN_X \subseteq A$ を得る。
帰納的な集合 $X$ に対し $\NN = \NN_X$ とする。
$0$ の構成
$0 \in \NN$ を $$0 = \varnothing$$ で定義する
後者関数 $s$ を構成する方法
写像 $s: \NN \rightarrow \NN$ を $$s(n) = n \cup \cbr{n}$$ によって定義する。
各 $n \in \NN$ に対し $n \in s(n)$ であり $n \subseteq s(n)$ でもある。
$(\NN, 0, s)$ がペアノシステムであること
(P1) ～ (P3) を満たすことを確認すればいいね
$0 \not\in s[\NN]$ である。
$\varnothing \not\in \iset{s(n)}{n \in \NN}$ を示す。つまり任意の $n \in \NN$ に対し$$s(n) \neq \varnothing$$であることを示せばいいが、これは $n \in s(n)$ からわかる。
$\NN$ の部分集合 $A$ が
を共に満たせば $A = \NN$ である。
仮定より $A$ は帰納的な集合なので $\NN = \NN_A$ である（命題１）。
$\NN_A$ の定義より $\NN_A \subseteq A$ だが仮定より $A \subseteq \NN$ なので $A = \NN$ である。
各 $n, m \in \NN$ に対し $n \in m$ ならば $n \subseteq m$ である。
命題４より、各 $n \in \NN$ に対し集合 $A_n$ を $$A_n = \iset{m \in \NN}{n \in m \implies n \subseteq m}$$ として $0 \in A_n$ と $s[A_n] \subseteq A_n$ を示せばいい。
$\varnothing$ すなわち $0$ はいかなる集合も要素に持たないので $n \not\in 0$ である。従って
「$n \in 0 \implies n \subseteq 0$」
という命題は真であり、$0 \in A_n$ である。
$m \in A_n$ を任意に取り、$s(m) \in A_n$ であること、すなわち
$n \in s(m)$ ならば $n \subseteq s(m)$
が成り立つことを示す。 $n \in s(m)$ とする。$s(m) = m \cup \cbr{m}$ なので
$n \in m$ または $n = m$
である。
$n \in m$ と $m \in A_n$ から $$n \subseteq m$$ がわかり、$m \subseteq s(m)$ なので $n \subseteq s(m)$ である。
$m \subseteq s(m)$ なので $n \subseteq s(m)$ を得る。
各 $n, m \in \NN$ に対し、$s(n) \subseteq s(m)$ ならば $n \subseteq m$ である。
$n \in s(n)$ なので仮定より $n \in s(m)$ であり、$s(m) = m \cup \cbr{m}$ なので
である。前者なら命題５より $n \subseteq m$ であり、後者でも $n \subseteq m$ である。
$s$ は単射である。
$(\NN, 0, s)$ はペアノシステムである。
$\NN$ の要素を自然数と呼ぶ。
ペアノの公理の一意性
今日の目標 ペアノシステムの一意性を示す。 ペアノシステムの一意性 前にペアノシステムを 「集合」で ...
https://sorai-note.com/math/200419/