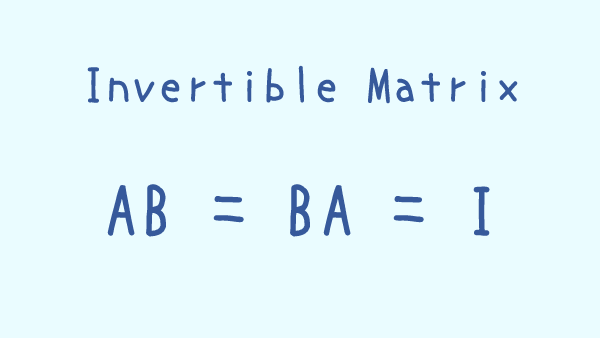行列式の理論の演習問題 18 問（解答付き）｜線形代数学

$A = (a_{i,j})_{i,j}$ とする。$S_3 = \cbr{\text{id}_3, (1\ 2), (1\ 3), (2\ 3), (1\ 2\ 3), (1\ 3\ 2)}$ なので

よって \begin{align} \det A &= \sum_{\sigma \in S_3} (\sgn \sigma) a_{1,\sigma(1)} a_{2,\sigma(2)} a_{3,\sigma(3)} \\&= 45 \minus 72 \minus 105 \minus 48 + 84 + 96 = 0 \end{align}

$S_2 = \cbr{\text{id}_2, (1\ 2)}$ なので

よって \begin{align} \det A &= \sum_{\sigma \in S_2} (\sgn \sigma) a_{1,\sigma(1)} a_{2,\sigma(2)} \\ &= a_{1,1} a_{2,2} \minus a_{1,2} a_{2,1} \end{align}

$S_3 = \cbr{\text{id}_3, (1\ 2), (1\ 3), (2\ 3), (1\ 2\ 3), (1\ 3\ 2)}$ なので

よって \begin{align} \det A &= \sum_{\sigma \in S_3} (\sgn \sigma) a_{1,\sigma(1)} a_{2,\sigma(2)} a_{3,\sigma(3)} \\ &= a_{1,1} a_{2,2} a_{3,3} + a_{1,2} a_{2,3} a_{3,1} + a_{1,3} a_{2,1} a_{3,2} \\ &\quad\qquad \minus a_{1,2} a_{2,1} a_{3,3} \minus a_{1,3} a_{2,2} a_{3,1} \minus a_{1,1} a_{2,3} a_{3,2} \end{align}

$I$ の $(i,j)$-成分を $a_{i,j}$ とすると、単位行列の定義より $$a_{i,j}= \begin{cases} 1 & (\text{$i = j$ のとき}) \\ 0 & (\text{$i \neq j$ のとき}) \end{cases} $$ である。置換 $\sigma$ が恒等置換 $\text{id}_n$ でないならば、$\sigma(k) \neq k$ となる $k$ が存在して $a_{k,\sigma(k)} = 0$ となるため $$a_{1,\sigma(1)} \cdots a_{n,\sigma(n)} = 0$$ となる。よって \begin{align} \det I &= \sum_{\sigma \in S_n} (\sgn \sigma) a_{1,\sigma(1)} \cdots a_{n,\sigma(n)} \\&= (\sgn \text{id}_n) a_{1,\text{id}_n(1)} \cdots a_{n,\text{id}_n(n)} \\&= 1 \end{align}

$\iset{\sigma}{\sigma \in S_n} = \iset{\sigma^{\minus 1}}{\sigma \in S_n}$ （※１） なので \begin{align} \text{(左辺)} &= \sum_{\sigma \in S_n} (\sgn \pbr{\sigma^{\minus 1}}) a_{1,\sigma^{\minus 1}(1)} \cdots a_{n,\sigma^{\minus 1}(n)} \end{align} である。ここで $\cbr{1, \cdots, n} = \cbr{\sigma(1), \cdots, \sigma(n)}$ を用いると \begin{align} a_{1,\sigma^{\minus 1}(1)} \cdots a_{n,\sigma^{\minus 1}(n)} &= a_{\sigma(1),\sigma^{\minus 1}(\sigma(1))} \cdots a_{\sigma(n),\sigma^{\minus 1}(\sigma(n))} \\&=a_{\sigma(1),1} \cdots a_{\sigma(n),n} \end{align} となり、また $\sgn \sigma = \sgn \pbr{\sigma^{\minus 1}}$ （※２） なので $\text{(左辺)} = \text{(右辺)}$ を得る。

問題２より前者だけ示せば十分。

左辺の行列を $A = (a_{i,j})_{i,j}$ とする。$i \lt j$ ならば $a_{i,j} = 0$ であることに注意。行列式の定義より \begin{align} \det A &= \sum_{\sigma \in S_n} (\sgn \sigma) a_{1,\sigma(1)} \cdots a_{n,\sigma(n)} \end{align} であるが、次が成り立つ。

よって $\text{id}_n$ でない置換 $\sigma$ に対しては $a_{i,\sigma(i)} = 0$ となる $i$ が存在するので $$a_{1,\sigma(1)} \cdots a_{n,\sigma(n)} = 0$$ となる。したがって \begin{align} \det A &= (\sgn \text{id}_n) a_{1,\text{id}_n(1)} \cdots a_{n,\text{id}_n(n)} \\&= a_{1,1} \cdots a_{n,n} \end{align}

一般には成り立たない。実際 $$A = \pbr{\begin{matrix} 1 & 0 \\ 0 & 0 \end{matrix}} \qquad B = \pbr{\begin{matrix} 0 & 0 \\ 0 & 1 \end{matrix}} $$ とすると $\det A + \det B = 0 + 0 = 0$ であるが、 $$A + B = \pbr{\begin{matrix} 1 & 0 \\ 0 & 1 \end{matrix}} $$ なので $\det(A + B) = 1$ である。

$\tau = (k\ \ell)$ とする。左辺の行列を $A$ とし、右辺の行列を $B = (b_{i,j})_{i,j}$ と書くと $b_{i,j} = a_{i,\tau(j)}$ であり、 \begin{align} \det B &= \sum_{\sigma \in S_n} (\sgn \sigma) b_{1, \sigma(1)} \cdots b_{n, \sigma(n)} \\&= \sum_{\sigma \in S_n} (\sgn \sigma) a_{1,\tau(\sigma(1))} \cdots a_{n,\tau(\sigma(n))} \\&= \sum_{\sigma \in S_n} (\minus \sgn \tau)(\sgn \sigma) a_{1,\tau(\sigma(1))} \cdots a_{n,\tau(\sigma(n))} \\&= \minus \sum_{\sigma \in S_n} (\sgn \tau \sigma) a_{1,(\tau \sigma)(1)} \cdots a_{n,(\tau \sigma)(n)} \end{align} となる。ここで $\iset{\sigma}{\sigma \in S_n} = \iset{\tau\sigma}{\sigma \in S_n}$ （※）を用いて \begin{align} \det B &= \minus \sum_{\sigma \in S_n} (\sgn \sigma) a_{1,\sigma(1)} \cdots a_{n,\sigma(n)} \\&=\minus \det A \end{align} となり $\det A = \minus \det B$ を得る。

この行列を $A$ とすると、$A$ の第 $k$ 列と第 $\ell$ 列を入れ替えても $A$ のままなので $$\det{A} = \minus \det{A}$$ となる（問題５）。よって $\det{A} = 0$ を得る。

転置行列の行列式を考えて（問題２）、 \begin{align} &\det \pbr{\begin{matrix} a_{1,1} & \cdots & a_{1, k \minus 1} & t b_1& a_{1,k+1} & \cdots & a_{1,n} \\\vdots & \ & \vdots& \vdots& \vdots& \ & \vdots \\a_{n,1} & \cdots & a_{n, k \minus 1} & t b_n & a_{n,k+1} & \cdots & a_{n,n} \end{matrix}} \\ \\ ={}&\sum_{\sigma \in S_n} (\sgn \sigma) a_{\sigma(1), 1} \cdots a_{\sigma(k \minus 1), k \minus 1} \cdot (t b_{\sigma(k)} ) \cdot a_{\sigma(k + 1), k + 1} \cdots a_{\sigma(n), n} \\ \\ = {}& t \sum_{\sigma \in S_n} (\sgn \sigma) a_{\sigma(1), 1} \cdots a_{\sigma(k \minus 1), k \minus 1} \cdot b_{\sigma(k)} \cdot a_{\sigma(k + 1), k + 1} \cdots a_{\sigma(n), n} \\ \\ ={}&t \cdot \det \pbr{\begin{matrix} a_{1,1} & \cdots & a_{1, k \minus 1} & b_1 & a_{1,k+1} & \cdots & a_{1,n} \\\vdots & \ & \vdots& \vdots& \vdots& \ & \vdots \\a_{n,1} & \cdots & a_{n, k \minus 1} & b_n & a_{n,k+1} & \cdots & a_{n,n} \end{matrix}} \end{align}

転置行列の行列式を考えて（問題２）、 \begin{align} &\det\pbr{\begin{matrix} a_{1,1} & \cdots & a_{1, k \minus 1} & b_1 + c_1 & a_{1,k+1} & \cdots & a_{1,n} \\\vdots & \ & \vdots& \vdots& \vdots& \ & \vdots \\a_{n,1} & \cdots & a_{n, k \minus 1} & b_n + c_n & a_{n,k+1} & \cdots & a_{n,n} \end{matrix}} \\ \\ ={}&\sum_{\sigma \in S_n} (\sgn \sigma) a_{\sigma(1), 1} \cdots a_{\sigma(k \minus 1), k \minus 1} \cdot (b_{\sigma(k)} + c_{\sigma(k)}) \cdot a_{\sigma(k + 1), k + 1} \cdots a_{\sigma(n), n} \\ \\ = {}& \sum_{\sigma \in S_n} (\sgn \sigma) a_{\sigma(1), 1} \cdots a_{\sigma(k \minus 1), k \minus 1} \cdot b_{\sigma(k)} \cdot a_{\sigma(k + 1), k + 1} \cdots a_{\sigma(n), n} \\&\quad + \sum_{\sigma \in S_n} (\sgn \sigma) a_{\sigma(1), 1} \cdots a_{\sigma(k \minus 1), k \minus 1} \cdot c_{\sigma(k)} \cdot a_{\sigma(k + 1), k + 1} \cdots a_{\sigma(n), n} \\ \\ ={}&\det\pbr{\begin{matrix} a_{1,1} & \cdots & a_{1, k \minus 1} & b_1 & a_{1,k+1} & \cdots & a_{1,n} \\\vdots & \ & \vdots& \vdots& \vdots& \ & \vdots \\a_{n,1} & \cdots & a_{n, k \minus 1} & b_n & a_{n,k+1} & \cdots & a_{n,n} \end{matrix}} \\ \\ &\qquad + \det\pbr{\begin{matrix} a_{1,1} & \cdots & a_{1, k \minus 1} & c_1 & a_{1,k+1} & \cdots & a_{1,n} \\\vdots & \ & \vdots& \vdots& \vdots& \ & \vdots \\a_{n,1} & \cdots & a_{n, k \minus 1} & c_n & a_{n,k+1} & \cdots & a_{n,n} \end{matrix}} \end{align}

この行列を $A = (a_{i,j})_{i,j}$ とすると、各 $i$ に対し $a_{i,\ell} = 0$ である。任意の $\sigma \in S_n$ に対し $\sigma(k) = \ell$ となる $k$ が存在して、このとき $a_{k,\sigma(k)} = 0$ となることから $$ \det A = \sum_{\sigma \in S_n} (\sgn \sigma) a_{1,\sigma(1)} \cdots a_{n,\sigma(n)} = 0 $$ となる。

$v_j = \pbr{\begin{matrix} a_{1, j} \\ \vdots \\ a_{n, j} \end{matrix} }$ $(j = 1, \ldots, n)$ と書くと、行列式の斉次性と加法性（問題７～７）より \begin{align} \text{(左辺)} &= t \cdot \det \overset{ \ \ (k) \quad\qquad \ (\ell) \ \ \ }{ \pbr{ \begin{matrix} v_1 & \cdots & v_k & \cdots & v_k & \ldots & v_n \end{matrix} } } \\ \\ & \qquad + \det \overset{ \ \ (k) \quad\qquad \ (\ell) \ \ \ }{ \pbr{ \begin{matrix} v_1 & \cdots & v_k & \cdots & v_\ell & \ldots & v_n \end{matrix} } } \end{align} となるが、2つの列が一致する行列式は $0$ なので（問題６）、$(\text{左辺}) = (\text{右辺})$ が得られる。

$A = (a_{i,j})_{i,j}$ および $B = (b_{i,j})_{i,j}$ と書き、$A$ の第 $j$ 列を $$v_j = \pbr{ \begin{matrix} a_{1, j} \\ \vdots \\ a_{n, j} \end{matrix} } \qquad(j = 1, \ldots, n) $$ と書くことにする。このとき $AB$ の第 $j$ 列は $$\pbr{\begin{matrix} a_{1,1}b_{1,j} + \cdots + a_{1,n}b_{n,j} \\ \vdots \\ a_{n,1}b_{1,j} + \cdots + a_{n,n}b_{n,j} \end{matrix}} = \sum_{i = 1}^n b_{i,j} v_i $$ と表されるので $$ \det{AB} = \det\pbr{ \begin{matrix} \ds\sum_{i = 1}^n b_{i,1} v_i & \cdots & \ds\sum_{i = 1}^n b_{i,n} v_i \end{matrix} } $$ であり、行列式の斉次性と加法性（問題７～７）より \begin{align} \det{AB} &= \sum_{i_1 = 1}^n \cdots \sum_{i_n = 1}^n \det\pbr{ \begin{matrix} b_{i_1, 1} v_{i_1} & \cdots & b_{i_n, n} v_{i_n} \end{matrix} } \\&= \sum_{i_1 = 1}^n \cdots \sum_{i_n = 1}^n b_{i_1,1} \cdots b_{i_n,n} \det\pbr{ \begin{matrix} v_{i_1} & \cdots & v_{i_n} \end{matrix} } \end{align} となる。更に2つの列が一致する行列の行列式は $0$ である（問題６）ので、$i_1, \ldots, i_n$ が互いに異なるような $(i_1, \ldots, i_n)$ に関する和を取ればよい。よって置換を用いて \begin{align} \det{AB} &= \sum_{\sigma \in S_n} b_{\sigma(1),1} \cdots b_{\sigma(n),n} \det\pbr{ \begin{matrix} v_{\sigma(1)} & \cdots & v_{\sigma(n)} \end{matrix} } \end{align} と表せる。また、行列の列を入れ替えるごとに行列式の値は $\minus 1$ 倍になるので（問題５） \begin{align} \det{AB} &= \sum_{\sigma \in S_n} b_{\sigma(1),1} \cdots b_{\sigma(n),n} \pbr{ (\sgn \sigma) \det\pbr{ \begin{matrix} v_1 & \cdots & v_n \end{matrix} } } \\ \\ &= \pbr{ \sum_{\sigma \in S_n} (\sgn \sigma) b_{\sigma(1),1} \cdots b_{\sigma(n),n}} \det\pbr{ \begin{matrix} v_1 & \cdots & v_n \end{matrix} } \\ \\ &= \det{\pbr{B^\top}}\det{A} =\det A \det B \end{align}

$n = k + \ell$ とし、左辺の行列を $A = (a_{i,j})_{i,j}$ とする。

まず右辺を式変形する。いま

$i,j \in \cbr{1, \ldots, \ell}$ に対し $a_{k + i,k + j} = b_{i,j}$

なので、右辺は \begin{align} &\mathrel{\phantom{=}} \det \pbr{ \begin{matrix} a_{1,1} & \cdots & a_{1, k} \\ \vdots & \ & \vdots \\ a_{k,1} & \cdots & a_{k, k} \end{matrix} } \det \pbr{ \begin{matrix} b_{1,1} & \cdots & b_{1,\ell} \\ \vdots & \ & \vdots \\ b_{\ell,1} & \cdots & b_{\ell,\ell} \end{matrix} } \\ \\ &= \pbr{\sum_{\tau \in S_k} (\sgn \tau) a_{1,\tau(1)} \cdots a_{k,\tau(k)}} \pbr{\sum_{\eta \in S_\ell} (\sgn \eta) b_{1,\eta(1)} \cdots b_{\ell,\eta(\ell)}} \\ \\ &= \sum_{\tau \in S_k}\sum_{\eta \in S_\ell} (\sgn \tau)(\sgn \eta) a_{1,\tau(1)} \cdots a_{k,\tau(k)} a_{k + 1,k + \eta(1)} \cdots a_{k + \ell,k + \eta(\ell)} \end{align} となる。

一方、左辺は $$\det A = \sum_{\sigma \in S_n} (\sgn \sigma) a_{1,\sigma(1)} \cdots a_{n,\sigma(n)}$$ であるが、いま $i \in \cbr{1, \ldots, k}, j \in \cbr{k + 1, \ldots, n}$ に対し $a_{i,j} = 0$ なので、$\sigma \in S_n$ で $\cbr{\sigma(1), \ldots, \sigma(k)} \neq \cbr{1, \ldots, k}$ なるものに対しては $$a_{1,\sigma(1)} \cdots a_{n,\sigma(n)} = 0$$ となる。よって $T_n = {\Big\{ {\sigma \in S_n} \,\Big|\, {\cbr{\sigma(1), \ldots, \sigma(k)} = \cbr{1, \ldots, k}} \Big\}}$ とすると $$\det A = \sum_{\sigma \in T_n} (\sgn \sigma) a_{1,\sigma(1)} \cdots a_{n,\sigma(n)}$$ と書ける。$\sigma \in T_n$ は集合 $\cbr{1, \ldots, k}$ をそれ自身に写し、また $\cbr{k + 1, \ldots, k + \ell}$ もそれ自身に写すので、各 $\sigma \in T_n$ に対し、$(\tau, \eta) \in S_k \times S_\ell$ で $$ \sigma = \pbr{ \begin{matrix} 1 & \cdots & k & k + 1 & \cdots & k + \ell \\ \tau(1) & \cdots & \tau(k) & k + \eta(1) & \cdots & k + \eta(\ell) \end{matrix} } $$ を満たすものが一意に存在する。 ここで $\tau$ を $m$ 個の互換の積、$\eta$ を $m’$ 個の互換の積で表せるとすると $\sigma$ は $m + m’$ 個の互換の積で表せるので $$\sgn \sigma = \sgn \tau \sgn \eta$$ である。したがって \begin{align} \det A ={} &\sum_{\sigma \in T_n} (\sgn \sigma) a_{1,\sigma(1)} \cdots a_{n,\sigma(n)} \\={} &\sum_{\tau \in S_k}\sum_{\eta \in S_\ell} (\sgn \tau)(\sgn \eta) a_{1,\tau(1)} \cdots a_{k,\tau(k)}a_{k+1,k+\eta(1)} \cdots a_{k+\ell,k + \eta(\ell)} \end{align} となり、左辺と右辺が等しいことが導かれた。

$A$ の第 $\ell$ 列は $$ \pbr{ \begin{matrix} a_{1, \ell} \\ \vdots \\ a_{n, \ell} \end{matrix} } = a_{1,\ell} \pbr{\begin{matrix} 1 \\ 0 \\ \vdots \\ 0 \end{matrix}} + \cdots + a_{n,\ell} \pbr{\begin{matrix} 0 \\ \vdots \\ 0 \\ 1 \end{matrix}} $$ と書けることに注意。よって行列式の斉次性と加法性（問題７～７）より、$\det A$ は \begin{align} \sum_{k = 1}^n a_{k,\ell} \det \pbr{ \begin{matrix} a_{1,1} & \cdots & a_{1, \ell \minus 1} & 0 & a_{1, \ell + 1} & \cdots & a_{1, n} \\ \vdots & & \vdots & \vdots & \vdots & & \vdots \\ a_{k \minus 1,1} & \cdots & a_{k \minus 1, \ell \minus 1} & 0 & a_{k \minus 1, \ell + 1} & \cdots & a_{k \minus 1, n} \\ a_{k,1} & \cdots & a_{k, \ell \minus 1} & 1 & a_{k, \ell + 1} & \cdots & a_{k, n} \\ a_{k + 1,1} & \cdots & a_{k + 1, \ell + 1} & 0 & a_{k + 1, \ell + 1} & \cdots & a_{k + 1, n} \\ \vdots & & \vdots & \vdots & \vdots & & \vdots \\ a_{n,1} & \cdots & a_{n, \ell \minus 1} & 0 & a_{n, \ell + 1} & \cdots & a_{n, n} \end{matrix} } \end{align} と等しくなる。ここで第 $1$ 列と第 $\ell$ 列を入れ替え、更に第 $1$ 行と第 $k$ 行を入れ替えると、 \begin{align} \sum_{k = 1}^n a_{k,\ell} \det \pbr{ \begin{matrix} 1 & a_{k,1} & \cdots & a_{k, \ell \minus 1} & a_{k, \ell + 1} & \cdots & a_{k, n} \\ 0 & a_{1,1} & \cdots & a_{1, \ell \minus 1} & a_{1, \ell + 1} & \cdots & a_{1, n} \\ \vdots & \vdots & & \vdots & \vdots & & \vdots \\ 0 & a_{k \minus 1,1} & \cdots & a_{k \minus 1, \ell \minus 1} & a_{k \minus 1, \ell + 1} & \cdots & a_{k \minus 1, n} \\ 0 & a_{k + 1,1} & \cdots & a_{k + 1, \ell + 1} & a_{k + 1, \ell + 1} & \cdots & a_{k + 1, n} \\ \vdots & \vdots & & \vdots & \vdots & & \vdots \\ 0 & a_{n,1} & \cdots & a_{n, \ell \minus 1} & a_{n, \ell + 1} & \cdots & a_{n, n} \end{matrix} } \end{align} となり（問題５）、左上の $1$ 次正方行列と右下の $(n \minus 1)$ 次正方行列に分解すると（問題１２）これは $\ds\sum_{k = 1}^n a_{k,\ell} A_{k, \ell}$ となる。

$A$ の第 $\ell$ 列を第 $k$ 列で置き換えた行列 $$B = \overset{(1) \qquad\qquad (k) \qquad\qquad (\ell) \qquad\qquad (n)}{ \pbr{\begin{matrix} a_{1,1} & \cdots & a_{1, k} & \cdots & a_{1,k} & \cdots & a_{1,n} \\\vdots & \ & \vdots& \ & \vdots& \ & \vdots \\a_{n,1} & \cdots & a_{n, k} & \cdots & a_{n,k} & \cdots & a_{n,n} \end{matrix}} } $$ を第 $\ell$ 列に沿って余因子展開すると $$ a_{1,k} B_{1,\ell} + \cdots + a_{n,k} B_{n,\ell} = \det B $$ となる（問題１３）が、$A$ と $B$ は第 $\ell$ 列以外はみな等しいので \begin{align} B_{1,\ell} &= A_{1,\ell} & &\cdots & B_{n,\ell} &= A_{n,\ell} \end{align} であり、また $B$ は第 $k$ 列と第 $\ell$ 列が一致するので $\det B = 0$ である（問題６）。よって $$ a_{1,k} A_{1,\ell} + \cdots + a_{n,k} A_{n,\ell} = 0 $$

$\det{A}\det\pbr{A^{\minus 1}} = \det\pbr{AA^{\minus 1}} = \det{I} = 1$ であり、$\det A \neq 0$ なので $$\det\pbr{A^{\minus 1}} = \dfrac{1}{\det A}$$ である。

$2n$ 次正方行列 $\pbr{ \begin{matrix} A & B \\ B & A \end{matrix} }$ に対し、各 $k = 1, \ldots, n$ について

第 $k$ 列の $1$ 倍を第 $n + k$ 列に加算

の操作を行っても行列式は変わらないので $$ \det\pbr{ \begin{matrix} A & B \\ B & A \end{matrix} } = \det\pbr{ \begin{matrix} A & B + A \\ B & A + B \end{matrix} } $$ である。さらにこの右辺の行列に対し、各 $k = 1, \ldots, n$ について

第 $n + k$ 行の $\minus 1$ 倍を第 $k$ 行に加算

の操作を行っても行列式は変わらないので $$ \det\pbr{ \begin{matrix} A & B + A \\ B & A + B \end{matrix} } = \det\pbr{ \begin{matrix} A \minus B & O \\ B & A + B \end{matrix} } $$ である。この値は $\det(A + B)\det(A \minus B)$ に等しい。

$2n$ 次正方行列 $\pbr{ \begin{matrix} A & B \\ \minus B & A \end{matrix} }$ に対し、各 $k = 1, \ldots, n$ について

第 $k$ 列の $i$ 倍を第 $n + k$ 列に加算

の操作を行っても行列式は変わらないので $$ \det\pbr{ \begin{matrix} A & B \\ B & A \end{matrix} } = \det\pbr{ \begin{matrix} A & B + iA \\ B & A + iB \end{matrix} } $$ である。さらにこの右辺の行列に対し、各 $k = 1, \ldots, n$ について

第 $n + k$ 行の $\minus i$ 倍を第 $k$ 行に加算

の操作を行っても行列式は変わらないので $$ \det\pbr{ \begin{matrix} A & B + iA \\ B & A + iB \end{matrix} } = \det\pbr{ \begin{matrix} A \minus iB & O \\ B & A + B \end{matrix} } $$ である。この値は $\det(A + iB)\det(A \minus iB)$ に等しい。