整列順序の基本
整列順序・狭義整列順序の基本を押さえる。
- $\NN$ を非負整数全体の集合とする。
最小元
半順序に関する最小元
半順序集合 $(X, \leq)$ において、$X$ の部分集合 $A$ の($\leq$ に関する)最小元とは
任意の $a \in A$ に対し $m \leq a$
を満たす $m \in A$ のことを言う。$\NN$ 上の通常の半順序 $\leq$ において、$2$ は $\cbr{2,3,5}$ の最小元である。実際 \begin{align} 2 \leq 2 && 2 \leq 3 && 2 \leq 5 \end{align} が成り立つ。
半順序集合 $(X, \leq)$ において、$X$ の部分集合 $A$ の $\leq$ に関する最小元は存在すれば唯一つ。
$m_1, m_2$ がともに $A$ の最小元であるとする。このとき $m_1$ の最小性より $$m_1 \leq m_2$$ であり、また $m_2$ の最小性より $$m_2 \leq m_1$$ である。よって $\leq$ の反対称律により $m_1 = m_2$ である。
半順序集合 $(X, \leq)$ において、$X$ の部分集合 $A$ の最小元を $\min A$ と書く。
狭義半順序に関する最小元
狭義半順序のときも同じように定義するの?
ダメな定義 $\quad$ 狭義半順序集合 $(X, \lt)$ において、$X$ の部分集合 $A$ の($\lt$ に関する)最小元とは
任意の $a \in A$ に対し $m \lt a$
を満たす $m \in A$ のことを言う。
$\lt$ に関する最小元が
常に存在しないことになっちゃう
狭義半順序 $\lt$ から半順序 $\leq$ を作って
そっちで最小性の判定をしてもらおう
集合 $X$ 上の狭義半順序 $\lt$ に対し、 $$x \leq y \defiff \text{$x \lt y$ または $x = y$}$$ で定義される $X$ 上の半順序 $\leq$ を、$\lt$ から誘導される半順序 と呼ぶ。
狭義半順序集合 $(X, \lt)$ において、$X$ の部分集合 $A$ の($\lt$ に関する)最小元を
$\lt$ から誘導される半順序 $\leq$ に関する $A$ の最小元
として定める。狭義半順序 $\lt$ から誘導される半順序 $\leq$ に対し \begin{align} \text{$m$ が $A$ の $\lt$ に関する最小元} &\iff \text{$m$ が $A$ の $\leq$ に関する最小元} \\ &\iff \text{任意の $a \in A$ に対し $m \leq a$} \\ &\iff \text{任意の $a \in A \setminus \cbr{m}$ に対し $m \lt a$ } \end{align}
狭義半順序集合 $(X, \lt)$ において、$X$ の部分集合 $A$ の $\lt$ に関する最小元は存在すれば唯一つ。
狭義半順序 $\lt$ による最小元とは $\lt$ から誘導される半順序 $\leq$ に関する最小元のことなので、命題1より一意性を得る。
整列順序
(I)
集合 $X$ 上の半順序 $\leq$ が整列順序であるとは、
$X$ の空でない部分集合が必ず $\leq$ に関する最小元を持つ
ことをいう。(II)
集合 $X$ 上の狭義半順序 $\lt$ が狭義整列順序であるとは、
$X$ の空でない部分集合が必ず $\lt$ に関する最小元を持つ
ことをいう。これはすなわち$\lt$ から誘導される半順序 $\leq$ が整列順序である
ことを意味する。勝手に全順序になる
整列順序は全順序である。
集合 $X$ 上の整列順序 $\leq$ に対し、$a, b \in X$ を任意に取ると $\cbr{a, b}$ は $X$ の空でない部分集合なので最小元を持ち、もし $a$ が最小元なら $a \leq b$ であり、$b$ が最小元なら $b \leq a$ である。
狭義整列順序は狭義全順序である。
$\lt$ を集合 $X$ 上の狭義整列順序とすると、$\lt$ から誘導される半順序 $\leq$ は $\lt$ の整列性より整列順序であり、命題3より $\leq$ は全順序である。誘導される半順序が全順序になるような狭義半順序は狭義全順序なので(※)、$\lt$ は狭義全順序である。
証明はこちら ↓
整列順序を備えた集合 $(X, \leq)$ を整列集合と呼ぶ。
空でない整列集合は最小元を持つ。
空でない整列集合 $X$ はそれ自身 $X$ の空でない部分集合であるので、整列順序の定義より $X$ は最小元を持つ。
整列集合の部分集合は、その順序によって整列集合となる。
整列集合 $(X, \leq)$ において、$X$ の部分集合 $X_0$ に対し、$X_0$ の空でない部分集合 $A$ は $X$ の空でない部分集合でもあるので、$\leq$ の整列性より $A$ は最小元を持つ。
整列順序の例
自然数全体の集合 $\NN$ は通常の全順序 $\leq$ によって整列集合である。
自然数 $n$ に関する命題
「$\NN$ の部分集合 $A$ が $n \in A$ を満たせば $A$ は最小元を持つ」
を数学的帰納法で示す。$0 \in A$ ならば任意の $n \in \NN$ に対し $0 \leq n$ なので、特に $0$ は $A$ の最小元である。
$\NN$ の部分集合 $A$ が $n + 1 \in A$ を満たしているとする。
Base Case と同じ。
$A_\minus = \iset{k \in \NN}{k + 1 \in A}$ とすると $n \in A_\minus$ なので、帰納法の仮定より $A_\minus$ は最小元 $m$ を持つ。 $a \in A$ を任意に取ると、$a \neq 0$ より $k + 1 = a$ なる $k \in \NN$ が存在し、$k \in A_\minus$ なので $m \leq k$ である。よって $$m + 1 \leq k + 1 = a$$ となる。更に $m \in A_\minus$ より $m + 1 \in A$ なので、$m + 1$ が $A$ の最小元である。
自然数全体の集合 $\NN$ 上の二項関係 $\rightarrow$ を次で定める。
$n, m \in \NN$ に対し、$n \rightarrow m$ とは
のいずれかが成り立つこと。
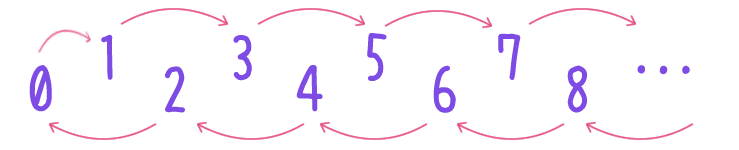
このとき $\rightarrow$ は全順序だが整列順序ではない。
「$n \rightarrow m$ かつ $n$ が奇数」ならば $m$ も奇数となることや、「$n \rightarrow m$ かつ $m$ が偶数」ならば $n$ も偶数となることに注意。
(i) と (ii) と $\leq$ の反射律から分かる。
$n \rightarrow m$ かつ $m \rightarrow n$ とすると、$n$ が奇数ならば $m$ も奇数であり、$n$ が偶数ならば $m$ も偶数である。よって (i) の場合でも (ii) の場合でも $\leq$ や $\geq$ の反対称律より $n = m$ となる。
$n \rightarrow m$ かつ $m \rightarrow k$ とする。
$m$ が奇数となり、更に $k$ も奇数となるので、$\leq$ の推移律から $n \rightarrow k$ である。
$k$ が奇数となり、(iii) より $n \rightarrow k$ である。
(iii) より $n \rightarrow k$ である。
(ii) と $\geq$ の推移律より $n \rightarrow k$ である。
$n,m \in \NN$ を任意に取る。$n$ と $m$ の偶奇が一致するときは $\leq$ や $\geq$ の全順序律から $n \leq m$ または $m \leq n$ である。 一方、$n$ が偶数で $m$ が奇数のときは $n \rightarrow m$ であり、 $n$ が奇数で $m$ が偶数のときは $m \rightarrow n$
$\NN$ の空でない部分集合として、非負偶数全体の集合 $E$ を考える。 $E$ の $\rightarrow$ に関する最小元とは
任意の $a \in E$ に対し $m \rightarrow a$
となるような $m \in E$ のことであるが、どの $m \in E$ に対しても $m \rightarrow m + 2$ は偽である。よって $E$ は $\rightarrow$ に関する最小元を持たず、したがって $\rightarrow$ は整列順序ではない。自然数全体の集合 $\NN$ の二項関係 $\rightarrow$ を次で定める。
$n, m \in \NN$ に対し、$n \rightarrow m$ とは
のどちらかが成り立つこと。
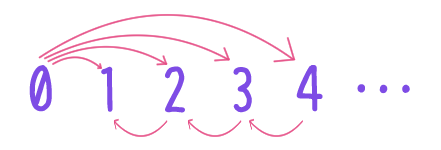
このとき $\rightarrow$ は全順序であり、$\NN$ は $\rightarrow$ に関して最小元を持つが、$\rightarrow$ は整列順序ではない。
$n \rightarrow 0$ のとき $n = 0$ となることに注意。$n \rightarrow m$ かつ $n \neq 0$ のとき $m \neq 0$ となることに注意。
(i) より $0 \rightarrow 0$ であり、$n \neq 0$ のときは (ii) より $n \rightarrow n$ となる。
$n \rightarrow m$ かつ $m \rightarrow n$ とする。$n = 0$ のときは $m \rightarrow 0$ より $m = 0$ である。$n \neq 0$ のときは $n \rightarrow m$ より $m \neq 0$ となり、$\geq$ の反射律より $n = m$ である。
$n \rightarrow m$ かつ $m \rightarrow k$ とする。
$m = 0$ となり、よって $n = 0$ となるので $n \rightarrow k$ である。
$n = 0$ となるので $n \rightarrow k$ である。
$n \rightarrow k$ は自明。
$\geq$ の推移律より $n \rightarrow k$ である。
$n, m \in \NN$ を任意に取る。$n = 0$ のときは $n \rightarrow m$ であり $m = 0$ のときは $m \rightarrow n$ である。$n,m \neq 0$ のときは $\geq$ の全順序律より $n \rightarrow m$ または $m\rightarrow n$ である。
任意の $n \in \NN$ に対し $0 \rightarrow n$ なので $0$ は $\NN$ の最小元である。
$\NN$ の空でない部分集合として $A = \NN \setminus \cbr{0}$ を考える。$A$ の $\rightarrow$ に関する最小元とは
任意の $k \in A$ に対して $m \rightarrow k$
となる $m \in A$ のことであるが、任意の $m \in A$ に対し $m \rightarrow m + 1$ は偽である。よって $A$ は $\rightarrow$ に関する最小元を持たず、$\rightarrow$ は整列順序でない。区間 $[0,1]$ は通常の順序で最小元を持つけど
その部分集合 $(0,1]$ は最小元を持たないから
整列順序にならないって言ってもいいかもね