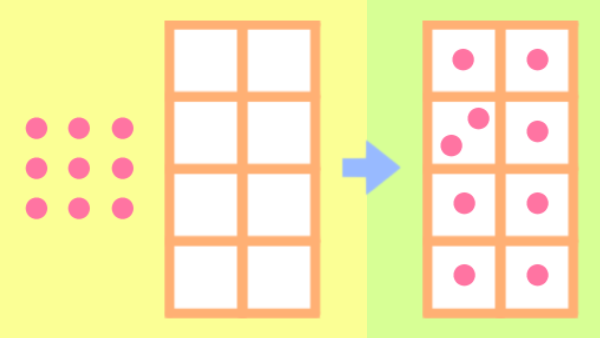
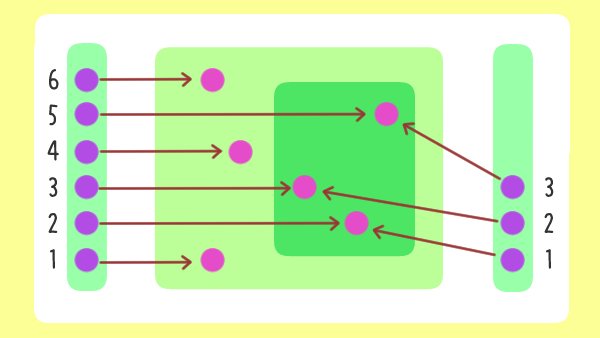
単射・全射・全単射の演習問題 35 問(解答付き)
単射・全射・全単射の扱いに慣れる。演習問題で証明を書けるようになる。
- 集合 $X$ のべき集合を $\mathcal{P}(X)$ で表す。
- 写像 $f: X \rightarrow Y$ に対し、$X$ の部分集合 $A$ の $f$ による像を $f(A)$ と書く。
- $\NN$ を非負整数全体の集合とする。
- $\NN_+$ を正整数全体の集合とする。
- $\ZZ$ を整数全体の集合とする。
- $\QQ$ を有理数全体の集合とする。
- $\QQ_+$ を正の有理数全体の集合とする。
- $\RR$ を実数全体の集合とする。
- $\NN[X]$ を非負整数係数 $1$ 変数多項式全体の集合とする。
- $\ZZ[X]$ を整数係数 $1$ 変数多項式全体の集合とする。
↓ の記事をどうぞ
定義の確認
$f: X \rightarrow Y$ とする。
$f$ が単射であるとは、 各 $x_1, x_2 \in X$ に対し $$f(x_1) = f(x_2) \implies x_1 = x_2$$ が成り立つこと。
$f$ が全射であるとは、 $f(X) = Y$ が成り立つこと。
$f$ が全単射であるとは、$f$ が単射でも全射でもあること。
$f(X) \subseteq Y$ は自明だから $Y \subseteq f(X)$ を示せばいい
$y \in f(X)$ であること
つまり $y = f(x)$ となる $x \in X$ が存在することを言えばいい
集合 $X$ とその部分集合 $A$ に対し、写像 $$\iota: A \rightarrow X, \qquad \iota(a) = a$$ を $A$ から $X$ への包含写像と呼ぶ。
特に $X$ から $X$ への包含写像を $X$ 上の恒等写像と呼び、$\text{id}_X$ と書く。すなわち $$\text{id}_X: X \rightarrow X, \qquad \text{id}_X(x) = x$$ である。
$f: X \rightarrow Y$ と $g: Y \rightarrow Z$ に対し、写像 $g \circ f: X \rightarrow Z$ を $$(g \circ f)(x) = g(f(x))$$ によって定める。これを $f$ と $g$ との合成写像と呼ぶ。
写像 $f: [\minus 1, 0] \rightarrow \RR$ を $f(x) = \abs{x}$ と定めたとき、$f$ が単射であることを示せ。
始域 $[\minus 1, 0]$ に属する二元 $x_1, x_2$ が $f(x_1) = f(x_2)$ を満たすとする。このとき $$\abs{x_1} = \abs{x_2}$$ なので $$\minus x_1 = \minus x_2$$ であり、したがって $x_1 = x_2$ である。よって $f$ は単射である。
写像 $f: [\minus 1, 2] \rightarrow \RR$ を $f(x) = \abs{x}$ と定めたとき、$f$ が単射でないことを示せ。
始域 $[\minus 1, 2]$ に属する二元として $x_1 = \minus 1$ と $x_2 = 1$ を取る。このとき $$f(x_1) = \abs{\minus 1} = 1$$ $$f(x_2) = \abs{1} = 1$$ より $f(x_1) = f(x_2)$ である。しかし $x_1 \neq x_2$ である。よって $f$ は単射ではない。
写像 $f: [\minus 1, 0] \rightarrow [0,1]$ を $f(x) = \abs{x}$ と定めたとき、$f$ が全射であることを示せ。
終域 $[0, 1]$ に属する元 $y$ を任意に取る。このとき始域 $[\minus 1, 0]$ に属する元 $x$ として $x = \minus y$ を取ると、 $$f(x) = \abs{\minus y} = y$$ となる。よって $f$ は全射である。
写像 $f: [\minus 1, 0] \rightarrow [0,2]$ を $f(x) = \abs{x}$ と定めたとき、$f$ が全射でないことを示せ。
終域 $[0,2]$ に属する元として $y = 2$ を取る。このとき始域 $[\minus 1, 0]$ に属する任意の元 $x$ に対し $$f(x) = \abs{x} \leq 1 \lt 2 = y$$ となるので $f(x) \neq y$ である。よって $f$ は全射ではない。
演習問題
集合 $X$ とその部分集合 $A$ に対し、包含写像 $\iota: A \rightarrow X$ は単射であることを示せ。
$\iota(a_1) = \iota(a_2)$ となる $a_1, a_2 \in A$ を取ると、 $$a_1 = \iota(a_1) = \iota(a_2) = a_2$$ となるので、$\iota$ は単射である。
集合 $X$ 上の恒等写像 $\text{id}_X: X \rightarrow X$ は全単射であることを示せ。
$\text{id}_X$ は $X$ から $X$ への包含写像なので、問題1より単射である。
$x \in X$ を任意に取ると、$\text{id}_X(x) = x$ より $x \in \text{id}_X(X)$ となるので $\text{id}_X$ は全射である。
始域と終域が等しい単射は常に全単射か?
そうとは限らない。反例として $f: \NN \rightarrow \NN$ を $$f(n) = n+1$$ と定めると、$f(n_1) = f(n_2)$ となる $n_1, n_2 \in \NN$ に対し、$n_1 + 1 = n_2 + 1$ すなわち $n_1 = n_2$ となるので $f$ は単射である。一方 $f(n) = 0$ となる $n \in \NN$ は存在せず $0 \not\in f(\NN)$ なので $f$ は全射ではない。
写像 $f: X \rightarrow Y$ は全単射であるとする。このとき任意の $y \in Y$ に対し
$f(x) = y$ となる $x \in X$ が唯一つ存在する
ことを示せ。
$y \in Y$ を任意に取る。
$f$ が全射なので $y \in f(X)$ である。よって $f(x) = y$ となる $x \in X$ が存在する。
$f(x_1) = y$ かつ $f(x_2) = y$ となる $x_1, x_2 \in X$ に対し $$f(x_1) = f(x_2)$$ であり、$f$ の単射性より $x_1 = x_2$ となる。
$f: X \rightarrow Y$ と $g: Y \rightarrow Z$ に対し、
$g \circ f$ は単射 $\quad$ ならば $\quad$ $f$ は単射
であることを示せ。$x_1, x_2 \in X$ に対し $f(x_1) = f(x_2)$ であるとすると、 $$g(f(x_1)) = g(f(x_2))$$ すなわち $(g \circ f)(x_1) = (g \circ f)(x_2)$ であり、$g \circ f$ は単射なので $x_1 = x_2$ である。
$f: X \rightarrow Y$ と $g: Y \rightarrow Z$ に対し、
$g \circ f$ は全射 $\quad$ ならば $\quad$ $g$ は全射
であることを示せ。$z \in Z$ を任意に取る。このとき $g \circ f$ の全射性より $$g(f(x)) = z$$ となる $x \in X$ が存在し、$z \in g(Y)$ となるので $g$ は全射である。
$f: X \rightarrow Y$ と $g: Y \rightarrow Z$ に対し、
$g \circ f$ は単射 $\quad$ ならば $\quad$ $g$ は単射
は一般に成り立つか?一般には成り立たない。反例として $X = \cbr{0}, Y = \cbr{0,1}, Z = \cbr{0}$ および $$ \begin{aligned} f(0) &= 0 & g(0) &= 0 & g(1) &= 0 \end{aligned} $$ とすると $$(g \circ f)(0) = 0$$ であり、$g \circ f$ は単射であるが $g$ は単射ではない。
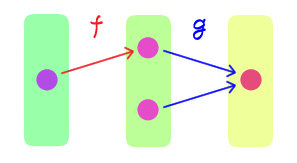
$f: X \rightarrow Y$ と $g: Y \rightarrow Z$ に対し、
$g \circ f$ は全射 $\quad$ ならば $\quad$ $f$ は全射
は一般に成り立つか?一般には成り立たない。 問題7の解答例で用いた反例において、$g \circ f$ は全射であるが $f$ は全射ではない。
$f: X \rightarrow Y$ と $g: Y \rightarrow X$ に対し、
$g \circ f = \text{id}_X$ $\quad$ ならば $\quad$ $f$ は単射 かつ $g$ は全射
が成り立つことを示せ。$f(x_1) = f(x_2)$ なる $x_1, x_2 \in X$ に対し $$x_1 = g(f(x_1)) = g(f(x_2)) = x_2$$ なので $f$ は単射。
$x \in X$ を任意に取る。このとき $g(f(x)) = x$ なので $x \in g(Y)$ である。
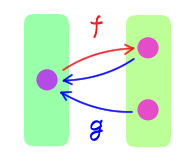
$f: X \rightarrow Y$ と $g: Y \rightarrow X$ に対し、
$g \circ f = \text{id}_X$ $\quad$ ならば $\quad$ $g$ は単射
は一般に成り立つか?一般には成り立たない。反例として $X = \cbr{0}, Y = \cbr{0, 1}$ とし、 \begin{align} f(0) = 0 && g(0) = 0 && g(1)=0 \end{align} とすると $$(g \circ f)(0) = 0$$ なので $g \circ f = \text{id}_{X}$ であるが $g$ は単射ではない。
一般には成り立たない。反例として $X = Y = \NN$ とし、 $$f(x) = x + 1, \qquad g(x) = \begin{cases} x \minus 1 & (\text{$x \geq 1$ のとき})\\ 0 & (\text{$x = 0$ のとき}) \end{cases} $$ とすると、各 $x \in \RR$ に対し $g(f(x)) = (x + 1) \minus 1 = x$ より $g \circ f = \text{id}_X$ であるが、 $$g(0) = 0 = g(1), \qquad 0 \neq 1$$ なので $g$ は単射ではない。
$f: X \rightarrow Y$ と $g: Y \rightarrow X$ に対し、
$g \circ f = \text{id}_X$ $\quad$ ならば $\quad$ $f$ は全射
は一般に成り立つか?一般には成り立たない。 問題10の解答例1(または解答例2)で用いた反例において、$g \circ f = \text{id}_X$ であるが $f$ は全射ではない。
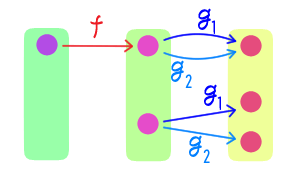
全単射写像 $f: X \rightarrow Y$ に対し、写像 $g: Y \rightarrow X$ で
をともに満たすものが唯一つ存在することを示せ。
$f$ は全単射なので、問題4より各 $y \in Y$ に対し
$f(x) = y$ となる $x \in X$ が唯一つ存在する。
この $x$ に対し $g(y) = x$ と定めることで写像 $g: Y \rightarrow X$ を定義する。
$x_0 \in X$ を任意に取る。このとき
$f(x) = f(x_0)$ となる $x \in X$
として $x_0$ が該当するので、$g$ の定義より $g(f(x_0)) = x_0$ である。
各 $y \in Y$ に対し $f(g(y)) = y$ となることは $g$ の定義から自明。
$g_1, g_2: Y \rightarrow X$ がともに (i),(ii) を満たすとする。$y \in Y$ を任意に取ると $f$ の全射性より $f(x) = y$ なる $x \in X$ が存在し、 $$g_1(y) = g_1(f(x)) = x = g_2(f(x)) = g_2(y)$$ となる。よって $g_1 = g_2$ である。
$f$ の逆写像と呼んで
$f^{-1}$ と書きます
$f: X \rightarrow Y$ と $g: Y \rightarrow Z$ に対し、
$f$ も $g$ も単射 $\quad$ ならば $\quad$ $g \circ f$ は単射
であることを示せ。$x_1, x_2 \in X$ が $(g \circ f)(x_1) = (g \circ f)(x_2)$ すなわち $$g(f(x_1)) = g(f(x_2))$$ であるとする。このとき $g$ の単射性より $f(x_1) = f(x_2)$ であり、更に $f$ の単射性より $x_1 = x_2$ である。よって $g \circ f$ は単射である。
$f: X \rightarrow Y$ と $g: Y \rightarrow Z$ に対し、
$f$ も $g$ も全射 $\quad$ ならば $\quad$ $g \circ f$ は全射
を示せ。$z \in Z$ を任意に取る。このとき $g$ の全射性より $g(y) = z$ となる $y \in Y$ が存在し、 $f$ の全射性より $f(x) = y$ となる $x \in X$ が存在する。 よって $$(g \circ f)(x) =g(f(x)) = g(y) = z$$ となるので $g \circ f$ は全射である。
$g \circ f$ も全単射
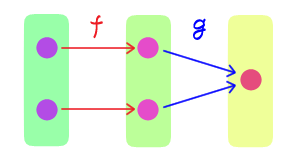
$f: X \rightarrow Y$ と $g: Y \rightarrow Z$ に対し、
$f$ が単射 $\quad$ ならば $\quad$ $g \circ f$ は単射
は一般に成り立つか?一般には成り立たない。反例として $X = \cbr{0, 1}, Y = \cbr{0,1}, Z = \cbr{0}$ とし、 $$\begin{aligned} f(0) &= 0 & f(1) &= 1 & g(0) &= 0 & g(1) &= 0 \end{aligned} $$ とすると \begin{align} (g \circ f)(0) &= 0 & (g \circ f)(1) &= 0 \end{align} であり、$f$ は単射であるが $g \circ f$ は単射ではない。
$f: X \rightarrow Y$ と $g: Y \rightarrow Z$ に対し、
$g$ が単射 $\quad$ ならば $\quad$ $g \circ f$ は単射
は一般に成り立つか?一般には成り立たない。反例として $X = \cbr{0, 1}, Y = \cbr{0}, Z = \cbr{0}$ とし、 $$\begin{aligned} f(0) &= 0 & f(1) &= 0 & g(0) &= 0 \end{aligned} $$ とすると \begin{align} (g \circ f)(0) &= 0 & (g \circ f)(1) &= 0 \end{align} であり、$g$ は単射であるが $g \circ f$ は単射ではない。
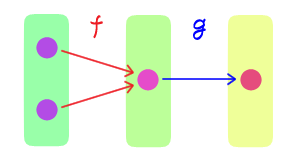
$f: X \rightarrow Y$ と $g: Y \rightarrow Z$ に対し、
$f$ が全射 $\quad$ ならば $\quad$ $g \circ f$ は全射
は一般に成り立つか?一般には成り立たない。反例として $X = \cbr{0}, Y = \cbr{0}, Z = \cbr{0,1}$ とし、 $$\begin{aligned} f(0) &= 0, \end{aligned} \qquad \begin{aligned} g(0) &= 0 \end{aligned} $$ とすると $$(g \circ f)(0) = 0$$ であり、$f$ は全射であるが、$g \circ f$ は全射ではない。
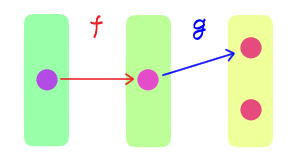
$f: X \rightarrow Y$ と $g: Y \rightarrow Z$ に対し、
$g$ が全射 $\quad$ ならば $\quad$ $g \circ f$ は全射
は一般に成り立つか?一般には成り立たない。反例として $X = \cbr{0}, Y = \cbr{0,1}, Z = \cbr{0,1}$ とし、 $$\begin{aligned} f(0) &= 0 & g(0) &= 0 & g(1) &= 1 \end{aligned} $$ とすると $$(g \circ f)(0) = 0$$ であり、$g$ は全射であるが、$g \circ f$ は全射ではない。
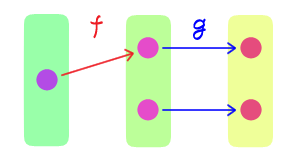
空でない集合 $X$ と集合 $Y$ に対し、
$X$ から $Y$ への単射が存在する$\quad$ ならば $\quad$ $Y$ から $X$ への全射が存在する
を示せ。$X \neq \varnothing$ より、$x_0 \in X$ を一つ取れる。単射 $f: X \rightarrow Y$ を取ると、その終域を狭めた写像 $f: X \rightarrow f(X)$ は全単射であり、その逆写像 $g: f(X) \rightarrow X$ が存在する。そこで $$h: Y \rightarrow X, \qquad h(y) = \begin{cases} g(y) & (y \in f(X)) \\ x_0 & (y \not\in f(X)) \end{cases}$$ を考える。$x \in X$ を任意に取ると $g$ の全射性より $g(y) = x$ なる $y \in f(X)$ が存在し、$h(y) = g(y) = x$ なので $h$ の全射性を得る。
$\varnothing$ から $Y$ への単射は存在する(空関数)けど
$Y$ から $\varnothing$ への全射は存在しない(そもそも写像がない)
選択公理を仮定する。集合 $X, Y$ に対し、
$X$ から $Y$ への全射が存在する$\quad$ ならば $\quad$ $Y$ から $X$ への単射が存在する
を示せ。
全射 $f: X \rightarrow Y$ を取ると、各 $y \in Y$ に対し、 $$\iset{x \in X}{f(x) = y} \neq \varnothing$$ であるので、選択公理より、関数 $g: Y \rightarrow X$ で
各 $y \in Y$ に対し $f(g(y)) = y$
となるものが存在する。このとき $g(a) = g(b)$ となる $a,b \in Y$ に対し $$a = f(g(a)) = f(g(b)) = b$$ となるので $g$ は単射である。$f_1, f_2: X \rightarrow Y$ と $g: Y \rightarrow Z$ に対し、
$g$ が単射 かつ $g \circ f_1 = g \circ f_2$ $\quad$ ならば $\quad$ $f_1 = f_2$
であることを示せ。$x \in X$ を任意に取る。$g \circ f_1 = g \circ f_2$ より $$g(f_1(x)) = g(f_2(x))$$ であり、$g$ が単射なので $f_1(x) = f_2(x)$ を得る。
$f_1, f_2: X \rightarrow Y$ と $g: Y \rightarrow Z$ に対し、
$g \circ f_1 = g \circ f_2$ $\quad$ ならば $\quad$ $f_1 = f_2$
は一般に成り立つか?一般には成り立たない。反例として $X = \cbr{0}, Y = \cbr{0,1}, Z = \cbr{0}$ とし、 \begin{aligned} f_1(0) &= 0 & f_2(0) &= 1 & g(0) &= 0 & g(1) &= 0 \end{aligned} とすると、 \begin{align} g(f_1(0)) = 0 && g(f_2(0)) = 0 \end{align} であり、$f_1 \neq f_2$ だが $g \circ f_1 = g \circ f_2$ である。
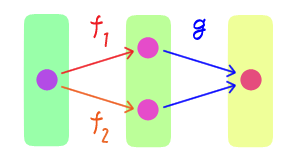
$f: X \rightarrow Y$ と $g_1, g_2: Y \rightarrow Z$ に対し、
$f$ が全射 かつ $g_1 \circ f = g_2 \circ f$ $\quad$ ならば $\quad$ $g_1 = g_2$
であることを示せ。$y \in Y$ を任意に取る。$f$ の全射性より $f(x) = y$ となる $x \in X$ が存在し、$g_1 \circ f = g_2 \circ f$ より $$g_1(f(x)) = g_2(f(x))$$ であり、 $g_1(y) = g_2(y)$ を得る。
$f: X \rightarrow Y$ と $g_1, g_2: Y \rightarrow Z$ に対し、
$g_1 \circ f = g_2 \circ f$ $\quad$ ならば $\quad$ $g_1 = g_2$
は一般に成り立つか?一般には成り立たない。反例として $X = \cbr{0}, Y = \cbr{0,1}, Z = \cbr{0,1,2}$ とし、 $$\begin{aligned} f(0) &= 0 & \begin{aligned} g_1(0) &= 0 \\ g_1(1) &= 1 & \end{aligned} & \begin{aligned} g_2(0) &= 0 \\ g_2(1) &= 2 & \end{aligned} \end{aligned}$$ とすると \begin{align} g_1(f(0)) = 0 && g_2(f(0)) = 0 \end{align} であり、$g_1 \neq g_2$ だが $g_1 \circ f = g_2 \circ f$ である。
$\NN^2$ から $\NN$ への全単射が存在することを示せ。
写像 $f: \NN^2 \rightarrow \NN$ を
$f(n,m) = a_{n + m} + n \quad$ ただし $\displaystyle\quad a_k = \sum_{i = 0}^k i$
で定め、この全単射性を示す。
$\ell \in \NN$ を任意に取る。$a_0 = 0$ であり、$\cbr{a_k}_{k \in \NN}$ は狭義単調増加な自然数列なので、 $$a_k \leq \ell \lt a_{k+1}$$ となる $k \in \NN$ が取れる。$n = \ell \minus a_k$ および $m = k \minus n$ とする。ここで $$0 \leq \ell \minus a_k \lt a_{k + 1} \minus a_k = k + 1$$ すなわち $0 \leq n \leq k$ であるので $n, m \in \NN$ であることに注意。したがって $$f(n,m) = a_k + (\ell \minus a_k) = \ell$$ である。
自然数 $n, m, n’, m’$ が $f(n, m) = f(n’, m’)$ を満たすとする。$a_{n + m + 1} = a_n + n + m + 1$ であることに注意すると、 $$a_{n + m} \leq f(n,m) \lt a_{n + m + 1}$$ $$a_{n’ + m’} \leq f(n’,m’) \lt a_{n’ + m’ + 1}$$ である。$f(n, m) = f(n’, m’)$ なので、$a_{n + m} \lt a_{n’ + m’ + 1}$ であり、数列 $\cbr{a_k}_{k \in \NN}$ は単調増加なので $n + m \lt n’ + m’ + 1$ すなわち $$n + m \leq n’ + m’$$ である。一方 $a_{n’ + m’} \lt a_{n + m + 1}$ なので、同様に $$n’ + m’ \leq n + m$$ である。したがって $n + m = n’ + m’$ である。ここで $$0 = f(n, m) \minus f(n’, m’) = n \minus n’$$ より $n = n’$ であり、したがって $m = m’$ である。
動画で詳しく解説してます(Youtube)↓
写像 $f: \NN^2 \rightarrow \NN$ を $$f(n,m) = 2^n(2m + 1) \minus 1$$ で定め、これが全単射であることを示す。
$k \in \NN$ を任意に取る。正整数 $k + 1$ の素因数分解により、 $$k + 1 = 2^{i}j$$ となる自然数 $i$ と正奇数 $j$ が存在することがわかる。ここで $n = i$ および $m = \dfrac{j \minus 1}{2}$ とすると、$n$ も $m$ も自然数で $$f(n,m) = 2^n(2m + 1) \minus 1 = 2^ij \minus 1 = (k + 1) \minus 1 = k$$ である。
自然数 $n, m, n’, m’$ が $f(n,m) = f(n’, m’)$ を満たすとする。すなわち $$2^n(2m + 1) = 2^{n’}(2m’ + 1)$$ とする。$2m + 1$ も $2m’ + 1$ も $2$ を素因数に持たないので、素因数分解の一意性より $n = n’$ であり、したがって $2m + 1 = 2m’ + 1$ すなわち $m = m’$ である。
動画で詳しく解説してます(Youtube)↓
ベルンシュタインの定理より、$\NN$ から $\NN^2$ への単射と $\NN^2$ から $\NN$ への単射の存在を示せばよい。
$f: \NN \rightarrow \NN^2, \ f(n) = (n,0)$ とすればよい。
$g: \NN^2 \rightarrow \NN$ を $g(n,m) = 2^n 3^m$ とすると素因数分解の一意性より $g$ は単射。
以下、自然数の「第 $i$ 桁目」とは「$10$ 進数表示したときの第 $i$ 桁目」のこととする。
自然数 $n$ の第 $i$ 桁目を $n_{[i]}$ と書く($i$ が $n$ の桁数を超えるときは $n_{[i]} = 0$)。例えば $$487_{[1]} = 7 \qquad 487_{[2]} = 8 \qquad 487_{[3]} = 4 \qquad 487_{[4]} = 0 \qquad \cdots $$ である。ここで写像 $f: \NN \rightarrow \NN^2$ を $$ f(n) = \pbr{ \sum_{i = 1}^\infty n_{[2i \minus 1]} \cdot 10^{i \minus 1}, \sum_{i = 1}^\infty n_{[2i]} \cdot 10^{i \minus 1} } $$ で定める。つまり自然数 $n$ の奇数桁だけを取り出した自然数と偶数桁だけを取り出した自然数との順序対を $f(n)$ とする。例えば \begin{align} f(12345) &= (135, 24) & f(10101212) &= (22, 1111) \end{align} である。
$(k, \ell) \in \NN^2$ を任意に取る。このとき $n \in \NN$ を、 $$n_{[2i \minus 1]} = k_{[i]} \qquad n_{[2i]} = \ell_{[i]}$$ となるように定めれば $f(n) = (k, \ell)$ となる。これは $$ n = \sum_{i = 1}^\infty k_{[i]} \cdot 10^{(2i \minus 1) \minus 1} + \sum_{i = 1}^\infty \ell_{[i]} \cdot 10^{2i \minus 1} $$ とすればよい。
$n \neq m$ とする。このとき $n$ と $m$ はある桁において異なる。つまり $$n_{[i]} \neq m_{[i]}$$ となる $i \geq 1$ が存在する。
$i$ が奇数のときは $f(n)$ の第 $1$ 成分において $\dfrac{i + 1}{2}$ 桁目が異なる。
$i$ が偶数のときは $f(n)$ の第 $2$ 成分において $\dfrac{i}{2}$ 桁目が異なる。
したがって $f(n) \neq f(m)$ である。
$\NN$ から $\ZZ$ への全単射が存在することを示せ。
写像 $f: \ZZ \rightarrow \NN$ を $$f(n) = \begin{cases} 2n \minus 1 & (\text{$n \geq 1$ のとき}) \\ \minus 2n & (\text{$n \leq 0$ のとき}) \end{cases} $$ で定める。
$f(n) = f(m)$ とする。
$f(m)$ も奇数なので $2n \minus 1 = 2m \minus 1$ となり、$n = m$ を得る。
$f(m)$ も偶数なので $\minus 2n = \minus 2m$ となり、$n = m$ を得る。
$m \in \NN$ を任意に取る。
$n = \dfrac{m + 1}{2}$ は $1$ 以上の整数であり $f\pbr{n} = 2n \minus 1 = m$ である。
$n = \minus \dfrac{m}{2}$ は $0$ 以下の整数であり $f\pbr{n} = \minus 2n = m$ である。
よって全単射 $f^{\minus 1}: \NN \rightarrow \ZZ$ が得られる。
ベルンシュタインの定理より、$\NN$ から $\ZZ$ への単射と $\ZZ$ から $\NN$ への単射の存在を示せばよい。
$\NN$ から $\ZZ$ への単射が存在することは自明($\NN$ から $\ZZ$ への包含写像)。
$\ZZ$ から $\NN$ への単射としては、写像 $f: \ZZ \rightarrow \NN$ を $$f(n) = \begin{cases} 2^n & (\text{$n \geq 0$ のとき}) \\ 3^{\abs n} & (\text{$n \lt 0$ のとき}) \end{cases} $$ で定めれば、$n \neq m$ のとき素因数分解の一意性より $f(n) \neq f(m)$ となるので $f$ は単射である。
$\NN_+$ から $\QQ_+$ への全単射が存在することを示せ。
素数列を $\cbr{p_n}_{n \in \NN}$ とする($p_0 = 2, p_1 = 3, p_2 = 5, \ldots$)。写像 $f: \NN[X] \rightarrow \NN_+$ を $$f\pbr{m_0 + m_1 X + \cdots + m_n X^n} = p_0^{m_0} p_1^{m_1} \cdots p_{n}^{m_{n}}$$ で定めると、素因数分解の一意性より $f$ は全単射。また写像 $g: \ZZ[X] \rightarrow \QQ_+$ を $$g\pbr{k_0 + k_1 X + \cdots + k_n X^n} = p_0^{k_0} p_1^{k_1} \cdots p_{n}^{k_{n}}$$ で定めると、素因数分解の一意性より $g$ も全単射。問題26より全単射 $H: \NN \rightarrow \ZZ$ が存在するので、これにより写像 $h: \NN[X] \rightarrow \ZZ[X]$ を \begin{align} &h\pbr{m_0 + m_1 X + \cdots + m_n X^n} \\ &\qquad \qquad = H(m_0) + H(m_1) X + \cdots + H(m_{n}) X^n \end{align} と定めると $h$ も全単射。よって $g \circ h \circ f^{\minus 1}: \NN_+ \rightarrow \QQ_+$ は全単射。
$\NN_+$ から $\QQ_+$ への単射が存在することは自明(包含写像)。
$q \in \QQ_+$ に対し $q$ の既約分数表示の分母を $D(q)$ と書き分子を $N(q)$ と書くことにする。このとき写像 $f: \QQ_+ \rightarrow \NN_+$ を $$f(q) = 2^{D(q)} 3^{N(q)}$$ と定めると、素因数分解の一意性より $f$ は単射。
よってベルンシュタインの定理より、$\NN_+$ から $\QQ_+$ への全単射が存在する。
$\NN$ から $\QQ$ への全単射が存在することを示せ。
問題27より、全単射 $f: \NN_+ \rightarrow \QQ_+$ が存在する。ここで写像 $F: \NN \rightarrow \QQ$ を $$F(n) = \begin{cases} f(n) & (\text{$n \gt 0$ のとき}) \\ 0 & (\text{$n = 0$ のとき}) \\ \minus f(\abs{n}) & (\text{$n \lt 0$ のとき}) \end{cases} $$ とすれば $F$ は全単射。
集合 $X, Y, Z$ は $X \subseteq Y \subseteq Z$ を満たし、$Z$ から $X$ への単射が存在するとする。
このとき $X$ から $Y$ への全単射、$Y$ から $Z$ への全単射、$X$ から $Z$ への全単射が存在することを示せ。
$X \subseteq Y \subseteq Z$ なので、包含写像を考えると
$X$ から $Y$ への単射が存在すること
$Y$ から $Z$ への単射が存在すること
$X$ から $Z$ への単射が存在すること
がわかる。一方 $Z$ から $X$ への単射が存在するという仮定を使って合成写像を考えると
$Y$ から $X$ への単射が存在すること
$Z$ から $Y$ への単射が存在すること
もわかる。以上により、ベルンシュタインの定理を用いて
$X$ から $Y$ への全単射が存在すること
$Y$ から $Z$ への全単射が存在すること
$Z$ から $X$ への全単射が存在すること
がわかる。
半開区間 $(0,1]$ から開区間 $(0,1)$ への全単射が存在することを示せ。
$(0,1]$ の部分集合 $A$ と $(0,1)$ の部分集合 $A’$ を \begin{align} A &= \cbr{1, \frac{1}{2}, \frac{1}{3}, \ldots} = \iset{\frac{1}{n}}{n \in \NN_+} \\ A’ &= \cbr{\frac{1}{2}, \frac{1}{3}, \frac{1}{4}, \ldots}= A \setminus \cbr{1} \end{align} とし、$B = (0,1] \setminus A$ とすると、 \begin{align} (0,1] &= A \cup B & A \cap B &= \varnothing \\ (0,1) &= A’ \cup B & A’ \cap B &= \varnothing \end{align}
となる。このとき \begin{align} f: A &\rightarrow A’, & f\pbr{\dfrac{1}{n}} &= \dfrac{1}{n+1} \\ g: B &\rightarrow B, & g(x) &= x \end{align} はどちらも全単射。よって写像 $h: (0,1] \rightarrow (0,1)$ を $$ h(x) = \begin{cases} f(x)& (\text{$x \in A$ のとき}) \\ g(x) & (\text{$x \in B$ のとき}) \end{cases} $$ と定めれば $h$ は全単射。
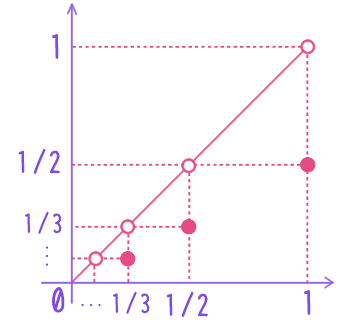
$(0,1]$ から $(0,1)$ への単射は $f(x) = \dfrac{x}{2}$ とすればよい。
$(0,1)$ から $(0,1]$ への単射は $g(x) = x$ とすればよい。
よってベルンシュタインの定理より、$(0,1]$ から $(0,1)$ への全単射が存在する。
$(0,1]$ から $(a,b]$ への全単射や
$(0,1)$ から $(a,b)$ への全単射を作ればいい
具体的には $\ell(x) = (b \minus a) x + a$
$a \lt c \lt b$ となる $c$ を取って
・$[a,c)$ から $(a,c)$ への全単射
・$\cbr{c}$ から $\cbr{c}$ への全単射
・$(c, b]$ から $(c,b)$ への全単射
を作って
場合分けを使って写像 $[a, b] \rightarrow (a,b)$ を定義すればいい
$X$ を集合、$\mathcal{P}(X)$ を $X$ のべき集合とする。
※ したがって $X$ から $\mathcal{P}(X)$ への全単射は存在しない。
全射 $f: X \rightarrow \mathcal{P}(X)$ が存在するとして矛盾を導く。$X$ の部分集合 $X_0$ を $$X_0 = \iset{x \in X}{x \not\in f(x)}$$ で定める。$f$ の全射性より $X_0 = f(y)$ となる $y \in X$ が存在する。
$X_0$ の定義より $y \not\in f(y)$ である一方 $y \in X_0 = f(y)$ なので矛盾。
$X_0$ の定義より $y \in f(y)$ である一方 $y \not\in X_0 = f(y)$ なので矛盾。
単射 $f: \mathcal{P}(X) \rightarrow X$ が存在すると仮定すると、$\mathcal{P}(X) \neq \varnothing$ より始域と終域が逆の全射 $f: X \rightarrow \mathcal{P}(X)$ が存在する(問題19)が、これは (1) に矛盾。
単射 $f: \mathcal{P}(X) \rightarrow X$ が存在するとして矛盾を導く。$X$ の部分集合 $X_0$ を $$X_0 = \iset{x \in X}{\text{$x = f(Y) \not\in Y$ なる $Y \in \mathcal{P}(X)$ が存在}}$$ で定める。
$X_0$ の定義より $f(X_0) = f(Y) \not\in Y$ となる $Y \in \mathcal{P}(X)$ が存在する。このとき $f$ の単射性より $X_0 = Y$ であり、$f(Y) \not\in Y$ より $f(X_0) \not\in X_0$ となり、矛盾。
$f(X_0) = f(X_0) \not\in X_0$ なので $X_0$ の定義より $f(X_0) \in X_0$ となり、矛盾。
「すべての集合からなる集合は存在しない」
を導ける
集合 $V$ が存在すると仮定すると
$\mathcal{P}(V) \subseteq V$ が成り立ち
包含写像を考えて $\mathcal{P}(V)$ から $V$ への単射が構成できる
でもこれはカントールの定理(問題31(2))に矛盾
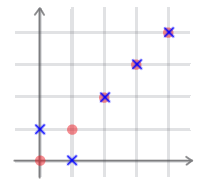
写像 $f, g: \NN \rightarrow \NN$ に対し $f + g, fg: \NN \rightarrow \NN$ を \begin{align} (f + g)(n) &= f(n) + g(n)\\ (fg)(n) &= f(n)g(n) \end{align} と定める。
$f, g: \NN \rightarrow \NN$ とする。このとき
$f$ も $g$ も単射 $\quad$ ならば $\quad$ $f + g$ も単射
は一般に成り立つか?一般には成り立たない。反例として \begin{align} f(n) = n && g(n) = \begin{cases} 1 & (\text{$n = 0$ のとき}) \\ 0 & (\text{$n = 1$ のとき}) \\ n & (\text{$n \geq 2$ のとき}) \end{cases} \end{align} とすると $f$ も $g$ も単射だが、 \begin{align} (f + g)(0) = 0 + 1 = 1 && (f + g)(1) = 1 + 0 = 1 \end{align} なので $f + g$ は単射ではない。
$f, g: \NN \rightarrow \NN$ とする。このとき
$f$ も $g$ も単射 $\quad$ ならば $\quad$ $fg$ も単射
は一般に成り立つか?一般には成り立たない。問題32の解答例で用いた反例において \begin{align} (fg)(0) = 0 \cdot 1 = 0 && (fg)(1) = 1 \cdot 0 = 0 \end{align} なので $fg$ は単射ではない。
$f, g: \NN \rightarrow \NN$ とする。このとき
$f$ も $g$ も全射 $\quad$ ならば $\quad$ $f + g$ も全射
は一般に成り立つか?一般には成り立たない。反例として \begin{align} f(n) = g(n) = n \end{align} とすると $f$ も $g$ も全射だが、 \begin{align} (f + g)(n) = 2n \end{align} であり $(f + g)(n) = 1$ となる $n$ が存在しないので $f + g$ は全射ではない。
$f, g: \NN \rightarrow \NN$ とする。このとき
$f$ も $g$ も全射 $\quad$ ならば $\quad$ $fg$ も全射
は一般に成り立つか?一般には成り立たない。問題34の解答例で用いた反例において \begin{align} (fg)(n) = n^2 \end{align} であり $(fg)(n) = 2$ となる $n$ が存在しないので $fg$ は全射ではない。